【题目】如图,八一广场要设计一个矩形花坛,花坛的长、宽分别为200m、120m,花坛中有一横两纵的通道,横、纵通道的宽度分别为3xm、2xm.
(1)用代数式表示三条通道的总面积S;当通道总面积为花坛总面积的 ![]() 时,求横、纵通道的宽分别是多少?
时,求横、纵通道的宽分别是多少?
(2)如果花坛绿化造价为每平方米3元,通道总造价为3168x元,那么横、纵通道的宽分别为多少米时,花坛总造价最低?并求出最低造价.(以下数据可供参考:852=7225,862=7396,872=7569)
参考答案:
【答案】
(1)
解:由题意得:
S=3x200+2x120×2-2×6x2=-12x2+1080x
由S= ![]() ×200×120,得:
×200×120,得:
∴-12x2+1080x= ![]() ×200×120,
×200×120,
即x2-90x+176=0,解得:x=2或x=88
又∵x>0,4x<200,3x<120,
∴解得0<x<40,
∴x=2,得横、纵通道的宽分别是6m、4m.
(2)
解:设花坛总造价为y元.
则y=3168x+(200×120-S)×3=3168x+(24000+12x2-1080x)×3
=36x2-72x+72000=36(x-1)2+71964,2·1·c·n·j·y
当x=1,即横、纵通道的宽分别为3m、2m时,花坛总造价最低,最低总造价为71964元.
【解析】(1)根据题意整理出二次函数的解析式,对于自变量的取值应该结合实际问题来解决.(2)注意对二次函数解析式整理时用顶点式进行整理简单
-
科目: 来源: 题型:
查看答案和解析>>【题目】我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育》的通知,通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为:“A—了解很多”,“B—了解较多”,“C—了解较少”,“D—不了解”),对本市一所中学的学生进行了抽样调查,我们将这次调查的结果绘制成以下两幅统计图.

根据以上信息,解答下列问题:
(1)本次抽样调查了多少名学生?
(2)补全两幅统计图;
(3)若该中学共有1 800名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较多”的有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个实际问题的函数图象的形状与y=
 的形状相同,且顶点坐标是(4,-2),那么它的函数解析式为( ).
的形状相同,且顶点坐标是(4,-2),那么它的函数解析式为( ).
A.y=
B.y= 或y=
或y= 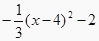
C.y=
D.y= 或y=
或y= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程: ①
 ; ②
; ② ; ③x2-y2=4;④5(x+y)=7(x+y);⑤2x2=3;⑥
; ③x2-y2=4;④5(x+y)=7(x+y);⑤2x2=3;⑥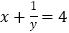 .其中是二元一次方程的是______(填序号).
.其中是二元一次方程的是______(填序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N.

(1)设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;
(2)当AE为何值时,四边形ADNM的面积最大?最大值是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】在解方程组
 时,由于粗心,甲看错了方程组中的a,而得到方程组的解为
时,由于粗心,甲看错了方程组中的a,而得到方程组的解为 ,乙看错了方程组中的b,而得到方程组的解为
,乙看错了方程组中的b,而得到方程组的解为 ,
,(1)甲把a看成了什么?乙把b看成了什么?
(2)求出原方程组的正确解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司试销一种成本为30元/件的新产品,按规定试销时的销售单价不低于成本单价,又不高于80元/件,试销中每天的销售量y(件)与销售单价x(元/件)满足下表中的函数关系.

(1)试求y与x之间的函数表达式;(2)设公司试销该产品每天获得的毛利润为S(元),求S与x之间的函数表达式(毛利润=销售总价-成本总价);
(2)当销售单价定为多少时,该公司试销这种产品每天获得的毛利润最大?
(3)最大毛利润是多少?此时每天的销售量是多少?
相关试题

