搜索
【题目】下列方程： ①
； ②
； ③x2-y2=4；④5（x+y）=7(x+y)；⑤2x2=3；⑥
．其中是二元一次方程的是______（填序号）．
参考答案：
【答案】①④
【解析】根据二元一次方程满足的条件：含有2个未知数，未知数的项的次数是1的整式方程一一判断即可.
①该方程中含有两个未知数，并且未知数的项的次数都是1的整式方程，所以它是二元一次方程；
②该方程是分式方程，所以它不是二元一次方程；
③该方程中的未知数的次数是2，所以它不是二元一次方程；
④由原方程得到2x+2y=0，该方程中含有两个未知数，并且未知数的项的次数都是1的整式方程，所以它是二元一次方程；
⑤该方程中含有一个未知数，所以它不是二元一次方程；
⑥该方程是分式方程，所以它不是二元一次方程；
综上所述，属于二元一次方程的是：①，④．
故答案是：①，④．
-
科目： 来源： 题型：
查看答案和解析>>【题目】操作与探究 探索：在如图1至图3中，△ABC的面积为a ．
（1）如图1, 延长△ABC的边BC到点D，使CD=BC，连结DA．若△ACD的面积为S1，则S1=________（用含a的代数式表示）；
（2）如图2，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE．若△DEC的面积为S2，则S2= （用含a的代数式表示）；
（3）在图2的基础上延长AB到点F，使BF=AB，连结FD，FE，得到△DEF（如图3）．若阴影部分的面积为S3，则S3=__________（用含a的代数式表示）．
发现：像上面那样，将△ABC各边均顺次延长一倍，连结所得端点，得到△DEF（如图3），此时，我们称△ABC向外扩展了一次．可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的_____倍．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我省教育厅下发了《在全省中小学幼儿园广泛深入开展节约教育》的通知，通知中要求各学校全面持续开展“光盘行动”.某市教育局督导检查组为了调查学生对“节约教育”内容的了解程度(程度分为：“A—了解很多”，“B—了解较多”，“C—了解较少”，“D—不了解”)，对本市一所中学的学生进行了抽样调查，我们将这次调查的结果绘制成以下两幅统计图.
根据以上信息，解答下列问题：
(1)本次抽样调查了多少名学生？
(2)补全两幅统计图；
(3)若该中学共有1 800名学生，请你估计这所中学的所有学生中，对“节约教育”内容“了解较多”的有多少名？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果一个实际问题的函数图象的形状与y=
的形状相同，且顶点坐标是(4，－2)，那么它的函数解析式为( )．
A.y=
B.y= 或y=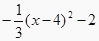 
C.y=
D.y= 或y= -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，八一广场要设计一个矩形花坛，花坛的长、宽分别为200m、120m，花坛中有一横两纵的通道，横、纵通道的宽度分别为3xm、2xm．
（1）用代数式表示三条通道的总面积S；当通道总面积为花坛总面积的
时，求横、纵通道的宽分别是多少？
（2）如果花坛绿化造价为每平方米3元，通道总造价为3168x元，那么横、纵通道的宽分别为多少米时，花坛总造价最低？并求出最低造价．（以下数据可供参考：852=7225，862=7396，872=7569） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，AB=2，E是AD边上一点（点E与点A，D不重合）．BE的垂直平分线交AB于M，交DC于N．
（1）设AE=x，四边形ADNM的面积为S，写出S关于x的函数关系式；
（2）当AE为何值时，四边形ADNM的面积最大？最大值是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】在解方程组
时，由于粗心，甲看错了方程组中的a，而得到方程组的解为
，乙看错了方程组中的b，而得到方程组的解为
，(1)甲把a看成了什么？乙把b看成了什么？
(2)求出原方程组的正确解.
相关试题
