【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
参考答案:
【答案】∠AOB; 垂直的定义; ∠COD; ∠AOB; ∠COD; ∠AOB; ∠COD.
【解析】
根据垂线的定义,可得∠AOB,根据等式的性质,可得∠COD,根据垂线的定义,可得答案.
∵OA⊥OB(已知)
所以∠AOB=90°(垂直的定义)
因为∠COD=∠AOD-∠AOC,∠AOB=∠BOC-∠AOC,∠AOD=∠BOC,
所以∠COD=∠AOB(等量代换)
所以∠COD=90°
所以OC⊥OD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OA⊥OC,OB⊥OD,∠AOD=5∠BOC,则∠AOD等于____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某年级380名师生秋游,计划租用7辆客车,现有甲、乙两种型号客车,它们的载客量和租金如表.
甲种客车
乙种客车
载客量(座/辆)
60
45
租金(元/辆)
550
450
(1)设租用甲种客车x辆,租车总费用为y元.求出y(元)与x(辆)之间的函数表达式;
(2)当甲种客车有多少辆时,能保障所有的师生能参加秋游且租车费用最少,最少费用是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点.
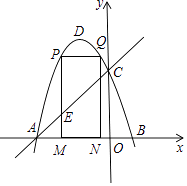
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过P作PQ∥AB交抛物线于点Q,过Q作QN⊥x轴于N,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方),若FG=2 DQ,求点F的坐标.
DQ,求点F的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a0=0
B.a+a2=a3
C.(2a)﹣(3a)=6a
D.2﹣1=
-
科目: 来源: 题型:
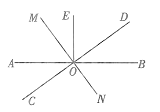
查看答案和解析>>【题目】如图,直线AB,CD,OE⊥AB,过点O画直线MN⊥CD. 若点F是直线MN上任意一点(点O除外),且∠AOC=34°.求∠EOF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,既是轴对称又是中心对称的图形是( )

A.4个
B.3个
C.2个
D.1个
相关试题

