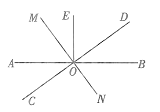
【题目】如图,直线AB,CD,OE⊥AB,过点O画直线MN⊥CD. 若点F是直线MN上任意一点(点O除外),且∠AOC=34°.求∠EOF的度数.
参考答案:
【答案】34°或146°
【解析】
当F在OM上时,根据垂直定义求出∠EOF=∠BOD,根据对顶角求出∠EOF=∠AOC,即可求出答案;当F在ON上时,求出∠AOM的度数,根据对顶角求出∠BON的度数,求出∠EOB+∠BON即可.
①当点F在射线OM上时,如图,
因为 OE⊥AB,MN⊥CD,
所以∠EOB=∠MOD=90°,
所以∠MOE+∠EOD=90°,∠EOD+∠BOD= 90°,
所以∠EOF=∠BOD=∠AOC=34°.
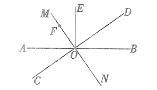
②当点F在射线ON上时,如图,
因为MN⊥CD,
所以 ∠MOC =∠AOC +∠AOM=90°,
所以 ∠AOM= 90°-34°=56°,
所以∠BON=∠AOM=56°
因为OE⊥AB,所以∠EOB=90°.
所以∠EOF=∠EOB+∠BON= 90°+56°=146°.
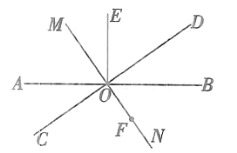
综上,∠EOF的度数是34°或146°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2﹣2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点.
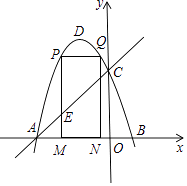
(1)求点A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过P作PQ∥AB交抛物线于点Q,过Q作QN⊥x轴于N,当矩形PMNQ的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方),若FG=2 DQ,求点F的坐标.
DQ,求点F的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OA⊥OB,∠AOD=∠BOC由此判定OC⊥OD,下面是推理过程,请填空.

解:∵OA⊥OB(已知)
所以_____=90°(________)
因为_____=∠AOD-∠AOC,____=∠BOC-∠AOC,∠AOD=∠BOC,
所以______=_____(等量代换)
所以______=90°
所以OC⊥OD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a0=0
B.a+a2=a3
C.(2a)﹣(3a)=6a
D.2﹣1=
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个图形中,既是轴对称又是中心对称的图形是( )

A.4个
B.3个
C.2个
D.1个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆O1、圆O2的半径不相等,圆O1的半径长为3,若圆O2上的点A满足AO1=3,则圆O1与圆O2的位置关系是( )
A.相交或相切
B.相切或相离
C.相交或内含
D.相切或内含
相关试题

