搜索
【题目】如图，矩形纸片ABCD中，AB=4，BC=6．将该矩形纸片剪去3个等腰直角三角形，所有剪法中剩余部分面积的最小值是（ ）
A.6
B.3
C.2.5
D.2
参考答案：
【答案】C
【解析】解：如图以BC为边作等腰直角三角形△EBC，延长BE交AD于F，得△ABF是等腰直角三角形，
作EG⊥CD于G，得△EGC是等腰直角三角形，
在矩形ABCD中剪去△ABF，△BCE，△ECG得到四边形EFDG，此时剩余部分面积的最小=4×6﹣ 
×4×4﹣ ×3×6﹣ ×3×3=2.5．
故选C．
以BC为边作等腰直角三角形△EBC，延长BE交AD于F，得△ABF是等腰直角三角形，作EG⊥CD于G，得△EGC是等腰直角三角形，在矩形ABCD中剪去△ABF，△BCE，△ECG得到四边形EFDG，此时剩余部分面积的最小本题考查几何最值问题、等腰直角三角形性质等知识，解题的关键是探究出如何确定三个等腰直角三角形，属于中考选择题中的压轴题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD的对角线AC，BD相交于点O，延长CB至点F，使CF=CA，连接AF，∠ACF的平分线分别交AF，AB，BD于点E，N，M，连接EO．
（1）已知BD=
，求正方形ABCD的边长；
（2）猜想线段EM与CN的数量关系并加以证明． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知点P（x0 ， y0）和直线y=kx+b，则点P到直线y=kx+b的距离证明可用公式d=
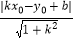计算．
例如：求点P（﹣1，2）到直线y=3x+7的距离．
解：因为直线y=3x+7，其中k=3，b=7．
所以点P（﹣1，2）到直线y=3x+7的距离为：d= =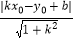 
= 
= 
．
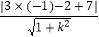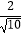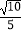根据以上材料，解答下列问题：
（1）求点P（1，﹣1）到直线y=x﹣1的距离；
（2）已知⊙Q的圆心Q坐标为（0，5），半径r为2，判断⊙Q与直线y=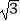
x+9的位置关系并说明理由；
（3）已知直线y=﹣2x+4与y=﹣2x﹣6平行，求这两条直线之间的距离． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知抛物线m：y=ax2﹣6ax+c（a＞0）的顶点A在x轴上，并过点B（0，1），直线n：y=﹣
x+ 
与x轴交于点D，与抛物线m的对称轴l交于点F，过B点的直线BE与直线n相交于点E（﹣7，7）．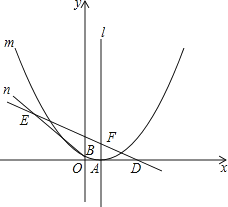
（1）求抛物线m的解析式；
（2）P是l上的一个动点，若以B，E，P为顶点的三角形的周长最小，求点P的坐标；
（3）抛物线m上是否存在一动点Q，使以线段FQ为直径的圆恰好经过点D？若存在，求点Q的坐标；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】某社区青年志愿者小分队年龄情况如下表所示：
年龄（岁）
18
19
20
21
22
人数
2
5
2
2
1
则这12名队员年龄的众数、中位数分别是（ ）
A.2，20岁
B.2，19岁
C.19岁，20岁
D.19岁，19岁 -
科目： 来源： 题型：
查看答案和解析>>【题目】剪纸是扬州的非物质文化遗产之一，下列剪纸作品中是中心对称图形的是（ ）
A.
B.
C.
D.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某电商销售一款夏季时装，进价40元/件，售价110元/件，每天销售20件，每销售一件需缴纳电商平台推广费用a元（a＞0）．未来30天，这款时装将开展“每天降价1元”的夏令促销活动，即从第1天起每天的单价均比前一天降1元．通过市场调研发现，该时装单价每降1元，每天销量增加4件．在这30天内，要使每天缴纳电商平台推广费用后的利润随天数t（t为正整数）的增大而增大，a的取值范围应为 ．
相关试题
