【题目】如图,正方形ABCD的对角线AC,BD相交于点O,延长CB至点F,使CF=CA,连接AF,∠ACF的平分线分别交AF,AB,BD于点E,N,M,连接EO.
(1)已知BD= ![]() ,求正方形ABCD的边长;
,求正方形ABCD的边长;
(2)猜想线段EM与CN的数量关系并加以证明.
参考答案:
【答案】
(1)
解:∵四边形ABCD是正方形,
∴△ABD是等腰直角三角形,
∴2AB2=BD2,
∵BD= ![]() ,
,
∴AB=1,
∴正方形ABCD的边长为1;
(2)
解:CN= ![]() CM.
CM.
证明:∵CF=CA,AF是∠ACF的平分线,
∴CE⊥AF,
∴∠AEN=∠CBN=90°,
∵∠ANE=∠CNB,
∴∠BAF=∠BCN,
在△ABF和△CBN中,
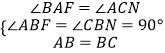 ,
,
∴△ABF≌△CBN(AAS),
∴AF=CN,
∵∠BAF=∠BCN,∠ACN=∠BCN,
∴∠BAF=∠OCM,
∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠ABF=∠COM=90°,
∴△ABF∽△COM,
∴ ![]() ,
,
∴ ![]() =
= ![]() ,
,
即CN= ![]() CM.
CM.
【解析】(1)根据正方形的性质以及勾股定理即可求得;(2)根据等腰三角形三线合一的性质证得CE⊥AF,进一步得出∠BAF=∠BCN,然后通过证得△ABF≌△CBN得出AF=CN,进而证得△ABF∽△COM,根据相似三角形的性质和正方形的性质即可证得CN= ![]() CM.本题考查了正方形的性质,勾股定理的应用,等腰三角形三线合一的性质,三角形全等的判定和性质,三角形相似的判定和性质,熟练掌握性质定理是解题的关键.
CM.本题考查了正方形的性质,勾股定理的应用,等腰三角形三线合一的性质,三角形全等的判定和性质,三角形相似的判定和性质,熟练掌握性质定理是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD⊥BC,CE⊥AB,垂足分别为D、E,AD、CE交于点H,请你添加一个适当的条件: , 使△AEH≌△CEB.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年6月15日是父亲节,某商店老板统计了这四年父亲节当天剃须刀销售情况,以下是根据该商店剃须刀销售的相关数据所绘制统计图的一部分.
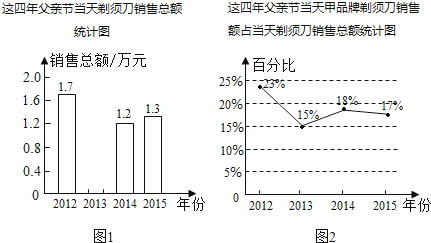
请根据图1、图2解答下列问题:
(1)近四年父亲节当天剃须刀销售总额一共是5.8万元,请将图1中的统计图补充完整;
(2)计算该店2015年父亲节当天甲品牌剃须刀的销售额. -
科目: 来源: 题型:
查看答案和解析>>【题目】某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:
 .
.
(1)求新坡面的坡角a;
(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆桥?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P(x0 , y0)和直线y=kx+b,则点P到直线y=kx+b的距离证明可用公式d=
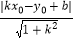 计算.
计算.
例如:求点P(﹣1,2)到直线y=3x+7的距离.
解:因为直线y=3x+7,其中k=3,b=7.
所以点P(﹣1,2)到直线y=3x+7的距离为:d=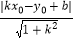 =
= 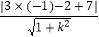 =
= 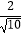 =
= 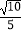 .
.
根据以上材料,解答下列问题:
(1)求点P(1,﹣1)到直线y=x﹣1的距离;
(2)已知⊙Q的圆心Q坐标为(0,5),半径r为2,判断⊙Q与直线y=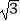 x+9的位置关系并说明理由;
x+9的位置关系并说明理由;
(3)已知直线y=﹣2x+4与y=﹣2x﹣6平行,求这两条直线之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线m:y=ax2﹣6ax+c(a>0)的顶点A在x轴上,并过点B(0,1),直线n:y=﹣
 x+
x+  与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).
与x轴交于点D,与抛物线m的对称轴l交于点F,过B点的直线BE与直线n相交于点E(﹣7,7).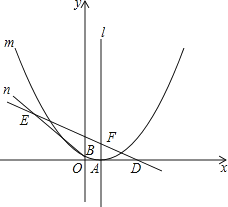
(1)求抛物线m的解析式;
(2)P是l上的一个动点,若以B,E,P为顶点的三角形的周长最小,求点P的坐标;
(3)抛物线m上是否存在一动点Q,使以线段FQ为直径的圆恰好经过点D?若存在,求点Q的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形纸片ABCD中,AB=4,BC=6.将该矩形纸片剪去3个等腰直角三角形,所有剪法中剩余部分面积的最小值是( )

A.6
B.3
C.2.5
D.2
相关试题

