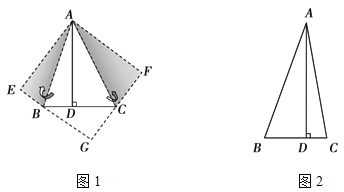
【题目】如图1,在△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长. 小萍同学灵活运用轴对称知识,将图形进行翻折变换如图1.她分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,得到四边形AEGF是正方形.设AD=x,利用勾股定理,建立关于x的方程模型,即可求出x的值.参考小萍的思路,探究并解答新问题:如图2,在△ABC中,∠BAC=30°,AD⊥BC于D,AD=4.请你按照小萍的方法画图,得到四边形AEGF,求△BGC的周长.(画图所用字母与图1中的字母对应)
参考答案:
【答案】![]() .
.
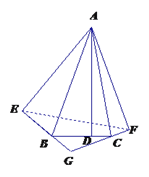
【解析】试题分析:参考做法得到四边形AEGF,连接EF得出△AEF为等边三角形,从而得出EF=4,∠FEG=∠EFG=30°,根据△EFG的性质求出EG的长度,最后根据BG+CG+BC=BG+CG+EB+FC=2EG得出三角形的周长.
试题解析:解: 参考小萍的做法得到四边形AEGF,∠EAF=60°,
∠EGF=120°,∠AEG=∠AFG= 90°,AE=AF=AD=4, 连结EF,可得 △AEF为等边三角形,
∴ EF=4, ∴ ∠FEG=∠EFG= 30°,∴ EG=FG,在△EFG中,可求![]() ,
,
∴△EFG的周长=BG+CG+BC=BG+CG+EB+FC=2EG=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 ,试判断BE与CF的位置关系,并说明你的理由.请补全下列说理过程.
,试判断BE与CF的位置关系,并说明你的理由.请补全下列说理过程.
解:BE ______ CF.
理由是:
 已知
已知 .
. ______
______  ______
______  垂直的定义
垂直的定义
 已知
已知 .
. =______
=______  .(等式的基本性质)
.(等式的基本性质)即
 ______
______  ______
______  ( ______________________
( ______________________ 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别是AB、BC上的点,且AE=BF.求证:CE=DF.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
 若
若 ,则
,则 的度数为______;
的度数为______; 若
若 ,求
,求 的度数;
的度数; 猜想
猜想 与
与 之间存在什么数量关系?并说明理由;
之间存在什么数量关系?并说明理由; 当
当 且点E在直线AC的上方时,这两块三角尺是否存在AD与BC平行的情况?若存在,请直接写出
且点E在直线AC的上方时,这两块三角尺是否存在AD与BC平行的情况?若存在,请直接写出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在□ABCD中,∠BAD的平分线交直线BC于点E,交直线DC于点F.
(1)在图1中证明
 ;
;(2)若
 ,G是EF的中点(如图2),直接写出∠BDG的度数;
,G是EF的中点(如图2),直接写出∠BDG的度数;(3)若
 ,FG∥CE,
,FG∥CE,  ,分别连结DB、DG(如图3),求∠BDG的度数.
,分别连结DB、DG(如图3),求∠BDG的度数.


-
科目: 来源: 题型:
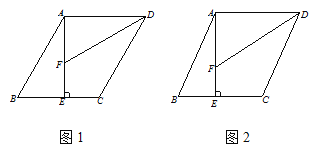
查看答案和解析>>【题目】已知在□ABCD中,AEBC于E,DF平分ADC 交线段AE于F.
(1)如图1,若AE=AD,ADC=60, 请直接写出线段CD与AF+BE之间所满足的等量关系;
(2)如图2, 若AE=AD,你在(1)中得到的结论是否仍然成立, 若成立,对你的结论加以证明, 若不成立, 请说明理由;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果二次三项式x2﹣16x+m2是一个完全平方式,那么m的值是( )
A.±8B.4C.±4D.8
相关试题

