【题目】![]() 特例研究:如图
特例研究:如图![]() ,等边
,等边![]() 的边长为8,求等边
的边长为8,求等边![]() 的高.
的高.
![]() 经验提升:
经验提升:
如图![]() ,在
,在![]() 中,
中,![]() ,点P为射线BC上的任一点,过点P作
,点P为射线BC上的任一点,过点P作![]() ,
,![]() ,垂足分别为D、E,过点C作
,垂足分别为D、E,过点C作![]() ,垂足为
,垂足为![]() 补全图形,判断线段PD,PE,CF的数量关系,并说明理由.
补全图形,判断线段PD,PE,CF的数量关系,并说明理由.
![]() 综合应用:
综合应用:
如图![]() ,在平面直角坐标系中有两条直线
,在平面直角坐标系中有两条直线![]() :
:![]() ,
,![]() :
:![]() ,若线段BC上有一点M到
,若线段BC上有一点M到![]() 的距离是1,请运用
的距离是1,请运用![]() 中的结论求出点M的坐标.
中的结论求出点M的坐标.

参考答案:
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]() 坐标为
坐标为![]() .
.
【解析】
![]() 利用等边三角形的性质和勾股定理即可得出结论;
利用等边三角形的性质和勾股定理即可得出结论;
![]() 利用面积法可以证明结论;
利用面积法可以证明结论;
![]() 连接AP,同理利用
连接AP,同理利用![]() 与
与![]() 面积之差等于
面积之差等于![]() 的面积可以证得结论;
的面积可以证得结论;
![]() 根据题意得到
根据题意得到![]() ,
,![]() ,
,![]() ,
,![]() ,根据图
,根据图![]() 的结论,求得M到AC的距离,即M点的纵坐标,再代入
的结论,求得M到AC的距离,即M点的纵坐标,再代入![]() 的解析式可求出M的坐标.
的解析式可求出M的坐标.
解:![]() 如图
如图![]() ,过点A作
,过点A作![]() 于G,
于G,

![]() 是等边三角形,
是等边三角形,![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
则等边![]() 的高为
的高为![]() ;
;![]() 当点P在边BC上时,
当点P在边BC上时,![]() ,
,
理由如下:如图![]() ,连接AP,
,连接AP,

![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() 当点P在BC的延长线上时,
当点P在BC的延长线上时,![]() ,
,
理由如下:如图![]() ,连接AP,
,连接AP,

![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;
;![]() 如图
如图![]() ,由题意可求得
,由题意可求得![]() ,
,![]() ,
,![]() ,
,

![]() ,
,![]() ,
,![]() ,
,![]() ,
,
过M分别作![]() 轴,
轴,![]() ,垂足分别为P、Q,
,垂足分别为P、Q,![]() 上的一点M到
上的一点M到![]() 的距离是1,
的距离是1,![]() ,
,
由图![]() 的结论得:
的结论得:![]() ,
,![]() ,
,![]() 点的纵坐标为2,
点的纵坐标为2,![]() 在直线
在直线![]() ,
,![]() 当
当![]() 时,
时,![]() ,
,![]() 坐标为
坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB =AC,AD⊥BC于点D,AM是△ABC的外角∠CAE的平分线.
(1)求证:AM∥BC;
(2)若DN平分∠ADC交AM于点N,判断△ADN的形状并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分表表示甲、乙两人与A地的距离
 、
、 与他们所行时间
与他们所行时间 之间的函数关系,且OP与EF相交于点M.
之间的函数关系,且OP与EF相交于点M. 求线段OP对应的
求线段OP对应的 与x的函数关系式;
与x的函数关系式; 求
求 与x的函数关系式以及A,B两地之间的距离;
与x的函数关系式以及A,B两地之间的距离; 求经过多少小时,甲、乙两人相距3km.
求经过多少小时,甲、乙两人相距3km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B是数轴上的两点.点P从原点出发,以每秒2个单位的速度向点B作匀速运动;同时,点Q也从原点出发用2s到达点A处,并在A处停留1s,然后按原速度向点B运动,速度为每秒4个单位.最终,点Q比点P早3s到达B处.设点P运动的时间为t s.

(1)点A表示的数为_________;当
 时,P、Q两点之间的距离为________个单位长度;
时,P、Q两点之间的距离为________个单位长度;(2)求点B表示的数;
(3)从P、Q两点同时出发至点P到达点B处的这段时间内,t为何值时,P、Q两点相距3个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为: y=
 x1 ,则tanA的值是 .
x1 ,则tanA的值是 . 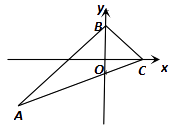
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边
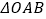 的边
的边 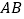 与
与 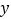 轴交于点
轴交于点 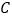 ,点
,点 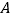 是反比例函数
是反比例函数 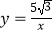
 图像上一点,若
图像上一点,若 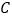 为
为 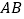 边的三等分点时,则等边
边的三等分点时,则等边 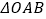 的边长为 .
的边长为 . 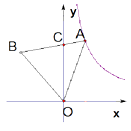
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系中,直线
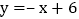 与直线
与直线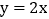 交与点
交与点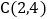 .
.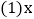 轴上是否存在点P,使
轴上是否存在点P,使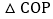 的面积是
的面积是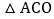 面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.
面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.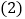 如图2,若点E是x轴上的一个动点,点E的横坐标为
如图2,若点E是x轴上的一个动点,点E的横坐标为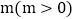 ,过点E作直线
,过点E作直线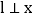 轴于点E,交直线
轴于点E,交直线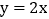 于点F,交直线
于点F,交直线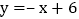 于点G,求m为何值时,
于点G,求m为何值时,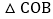 ≌
≌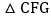 ?请说明理由.
?请说明理由. 在
在 的前提条件下,直线l上是否存在点Q,使
的前提条件下,直线l上是否存在点Q,使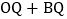 的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.
的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.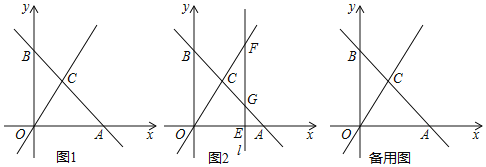
相关试题

