【题目】如图,在△ABC中,AB =AC,AD⊥BC于点D,AM是△ABC的外角∠CAE的平分线.
(1)求证:AM∥BC;
(2)若DN平分∠ADC交AM于点N,判断△ADN的形状并说明理由.

参考答案:
【答案】(1)证明见解析;(2)△ADN是等腰直角三角形,理由见解析
【解析】试题分析:(1)已知AB=AC,AD⊥BC,根据等腰三角形三线合一的性质可得∠BAD=∠CAD= ![]() ,再由AM平分∠EAC,根据角平分线的定义可得∠EAM=∠MAC=
,再由AM平分∠EAC,根据角平分线的定义可得∠EAM=∠MAC= ![]() ,根据平角的定义可得∠MAD=90°,根据同旁内角互补,两直线平行即可判定AM∥BC;(2)△ADN是等腰直角三角形,由(1)可得△ADN是直角三角形,因AM∥AD,根据平行线的性质可得∠AND=∠NDC,再由DN平分∠ADC,根据角平分线的定义和等量代换可得∠ADN=∠NDC=∠AND,根据等腰三角形的判定定理可得AD=AN,结论得证.
,根据平角的定义可得∠MAD=90°,根据同旁内角互补,两直线平行即可判定AM∥BC;(2)△ADN是等腰直角三角形,由(1)可得△ADN是直角三角形,因AM∥AD,根据平行线的性质可得∠AND=∠NDC,再由DN平分∠ADC,根据角平分线的定义和等量代换可得∠ADN=∠NDC=∠AND,根据等腰三角形的判定定理可得AD=AN,结论得证.
试题解析:
(1)∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD= ![]() .
.
∵AM平分∠EAC,
∴∠EAM=∠MAC= ![]() .
.
∴∠MAD=∠MAC+∠DAC= ![]() =
=![]() .
.
∵AD⊥BC,
∴![]() ,
,
∴∠MAD+![]() ,
,
∴AM∥BC.
(2)△ADN是等腰直角三角形,
理由是:∵AM∥AD,
∴∠AND=∠NDC,
∵DN平分∠ADC,
∴∠ADN=∠NDC=∠AND.
∴AD=AN.
∴△ADN是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和小慧两位同学在数学活动课中,把长为30cm,宽为10cm的长方形白纸条粘合起来,小明按如图甲所示的方法粘合起来得到长方形ABCD,粘合部分的长度为6cm,小慧按如图乙所示的方法粘合起来得到长方形 A1B1C1D1 ,粘合部分的长度为4cm。若长为30cm,宽为10cm的长方形白纸共有100张,则小明应分配到( )张长方形白纸条,才能使小明和小慧按各自粘合起来的长方形面积相等(要求100张长方形白纸条全部用完)


A.41
B.42
C.43
D.44 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级学生开展跳绳比赛活动,每班派5名学生参加,按团体总分多少排列名次,统计发现成绩最好的甲班和乙班总分相等,下表是甲班和乙班学生的比赛数据
 单位:个
单位:个
选手
1号
2号
3号
4号
5号
总计
甲班
100
98
105
94
103
500
乙班
99
100
95
109
97
500
此时有学生建议,可以通过考察数据中的其他信息作为参考,请解答下列问题:
 求两班比赛数据中的中位数,以及方差;
求两班比赛数据中的中位数,以及方差; 请根据以上数据,说明应该定哪一个班为冠军?为什么?
请根据以上数据,说明应该定哪一个班为冠军?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,弦AB的长等于⊙O的半径,那么弦AB所对的圆周角的度数 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分表表示甲、乙两人与A地的距离
 、
、 与他们所行时间
与他们所行时间 之间的函数关系,且OP与EF相交于点M.
之间的函数关系,且OP与EF相交于点M. 求线段OP对应的
求线段OP对应的 与x的函数关系式;
与x的函数关系式; 求
求 与x的函数关系式以及A,B两地之间的距离;
与x的函数关系式以及A,B两地之间的距离; 求经过多少小时,甲、乙两人相距3km.
求经过多少小时,甲、乙两人相距3km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B是数轴上的两点.点P从原点出发,以每秒2个单位的速度向点B作匀速运动;同时,点Q也从原点出发用2s到达点A处,并在A处停留1s,然后按原速度向点B运动,速度为每秒4个单位.最终,点Q比点P早3s到达B处.设点P运动的时间为t s.

(1)点A表示的数为_________;当
 时,P、Q两点之间的距离为________个单位长度;
时,P、Q两点之间的距离为________个单位长度;(2)求点B表示的数;
(3)从P、Q两点同时出发至点P到达点B处的这段时间内,t为何值时,P、Q两点相距3个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 特例研究:如图
特例研究:如图 ,等边
,等边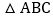 的边长为8,求等边
的边长为8,求等边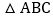 的高.
的高. 经验提升:
经验提升:如图
 ,在
,在 中,
中,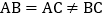 ,点P为射线BC上的任一点,过点P作
,点P为射线BC上的任一点,过点P作 ,
,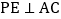 ,垂足分别为D、E,过点C作
,垂足分别为D、E,过点C作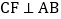 ,垂足为
,垂足为 补全图形,判断线段PD,PE,CF的数量关系,并说明理由.
补全图形,判断线段PD,PE,CF的数量关系,并说明理由. 综合应用:
综合应用:如图
 ,在平面直角坐标系中有两条直线
,在平面直角坐标系中有两条直线 :
: ,
,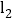 :
: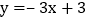 ,若线段BC上有一点M到
,若线段BC上有一点M到 的距离是1,请运用
的距离是1,请运用 中的结论求出点M的坐标.
中的结论求出点M的坐标.
相关试题

