【题目】如图,△ABC的内心在y轴上,点C的坐标为(2,0),点B的坐标为(0,2),直线AC的解析式为: y=![]() x1 ,则tanA的值是 .
x1 ,则tanA的值是 . 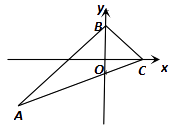
参考答案:
【答案】![]()
【解析】∵△ABC的内心在y轴上,
∴∠ABO=∠CBO,
又∵C(2,0),B(0,2),
∴BO=CO,BC=2![]() ,
,
∴∠BCO=∠CBO=45°,
∴∠ABC=90°,
又∵直线AC的解析式为: y=![]() x1 ,
x1 ,
∴设A(x,![]() x1 ),
x1 ),
∴AB2=x2+(![]() x3)2,AC2=(x-2)2+(
x3)2,AC2=(x-2)2+(![]() x1 )2,
x1 )2,
∴AB2+BC2=AC2,
∴x2+(![]() x3)2+8=(x-2)2+(
x3)2+8=(x-2)2+(![]() x1 )2,
x1 )2,
∴x=-6,
∴y=-4,
∴A(-6,-4),
∴AB=6![]() ,
,
∴tanA=![]() =
=![]() =
=![]() .
.
所以答案是:![]() .
.
【考点精析】利用勾股定理的概念和锐角三角函数的定义对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图的折线OPQ和线段EF,分表表示甲、乙两人与A地的距离
 、
、 与他们所行时间
与他们所行时间 之间的函数关系,且OP与EF相交于点M.
之间的函数关系,且OP与EF相交于点M. 求线段OP对应的
求线段OP对应的 与x的函数关系式;
与x的函数关系式; 求
求 与x的函数关系式以及A,B两地之间的距离;
与x的函数关系式以及A,B两地之间的距离; 求经过多少小时,甲、乙两人相距3km.
求经过多少小时,甲、乙两人相距3km.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A,B是数轴上的两点.点P从原点出发,以每秒2个单位的速度向点B作匀速运动;同时,点Q也从原点出发用2s到达点A处,并在A处停留1s,然后按原速度向点B运动,速度为每秒4个单位.最终,点Q比点P早3s到达B处.设点P运动的时间为t s.

(1)点A表示的数为_________;当
 时,P、Q两点之间的距离为________个单位长度;
时,P、Q两点之间的距离为________个单位长度;(2)求点B表示的数;
(3)从P、Q两点同时出发至点P到达点B处的这段时间内,t为何值时,P、Q两点相距3个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 特例研究:如图
特例研究:如图 ,等边
,等边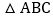 的边长为8,求等边
的边长为8,求等边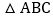 的高.
的高. 经验提升:
经验提升:如图
 ,在
,在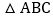 中,
中,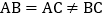 ,点P为射线BC上的任一点,过点P作
,点P为射线BC上的任一点,过点P作 ,
,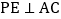 ,垂足分别为D、E,过点C作
,垂足分别为D、E,过点C作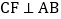 ,垂足为
,垂足为 补全图形,判断线段PD,PE,CF的数量关系,并说明理由.
补全图形,判断线段PD,PE,CF的数量关系,并说明理由. 综合应用:
综合应用:如图
 ,在平面直角坐标系中有两条直线
,在平面直角坐标系中有两条直线 :
: ,
,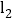 :
: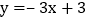 ,若线段BC上有一点M到
,若线段BC上有一点M到 的距离是1,请运用
的距离是1,请运用 中的结论求出点M的坐标.
中的结论求出点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边
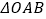 的边
的边 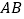 与
与 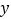 轴交于点
轴交于点 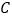 ,点
,点 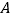 是反比例函数
是反比例函数 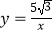
 图像上一点,若
图像上一点,若 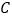 为
为 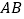 边的三等分点时,则等边
边的三等分点时,则等边 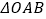 的边长为 .
的边长为 . 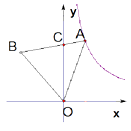
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,平面直角坐标系中,直线
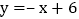 与直线
与直线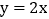 交与点
交与点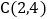 .
.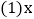 轴上是否存在点P,使
轴上是否存在点P,使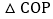 的面积是
的面积是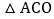 面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.
面积的二倍?若存在,直接写出点P的坐标;若不存在,说明理由.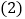 如图2,若点E是x轴上的一个动点,点E的横坐标为
如图2,若点E是x轴上的一个动点,点E的横坐标为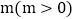 ,过点E作直线
,过点E作直线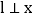 轴于点E,交直线
轴于点E,交直线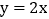 于点F,交直线
于点F,交直线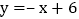 于点G,求m为何值时,
于点G,求m为何值时,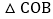 ≌
≌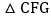 ?请说明理由.
?请说明理由. 在
在 的前提条件下,直线l上是否存在点Q,使
的前提条件下,直线l上是否存在点Q,使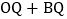 的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.
的值最小?若存在,直接写出点Q的坐标;若不存在,说明理由.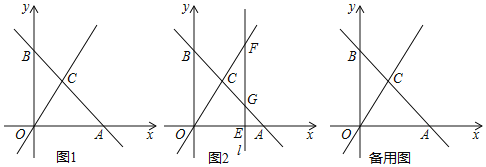
-
科目: 来源: 题型:
查看答案和解析>>【题目】汽车油箱中的余油量
 (升
(升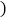 是它行驶的时间
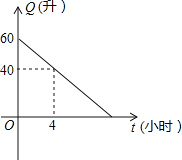
是它行驶的时间 (小 时) 的一次函数 . 某天该汽车外出时, 油箱中余油量与行驶时间的变化关系如图:
(小 时) 的一次函数 . 某天该汽车外出时, 油箱中余油量与行驶时间的变化关系如图:(1) 根据图象, 求油箱中的余油
 与行驶时间
与行驶时间 的函数关系 .
的函数关系 .(2) 从开始算起, 如果汽车每小时行驶 40 千米, 当油箱中余油 20 升时, 该汽车行驶了多少千米?
相关试题

