【题目】已知b是最小的正整数,且a、c满足|a+1|+(c+6)2=0.
(1)填空:a= ,b= ,c= ;
(2)a、b、c在数轴上所对应的点分别为A、B、C,P是数轴上点A、B之间一动点(不与点A、B重合),其对应的数为x,|x+1|+|x﹣1|= ;
(3)在(1)、(2)的条件下,点A、B、C开始在数轴上同时运动,若点C和点A分别以每秒6个单位长度和2个单位长度的速度向左运动,点B以每秒2个单位长度的速度向右运动,假设t秒钟过后,若点A与点C之间的距离表示为AC,点A与B之间的距离表示为AB.请问:AC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.

参考答案:
【答案】(1)-1;1;-6 (2)2 (3)不变;3
【解析】
(1)根据最小的正整数是1,推出b=1,再利用非负数的性质求出a、c即可.
(2)首先确定x的范围,再化简绝对值即可.
(3)AC﹣AB的值不变.根据题意用t表示出AC、AB即可解决问题.
解:(1)∵b是最小的正整数,
∴b=1,
∵|a+1|+(c+6)2=0,a+1=0,c+6=0,
∴a=-1, b=1,c=-6,
故答案为:-1,1,-6;
(2)由题意-1<x<1,
∴|x+1|+|x﹣1|=x+1-(x-1)= x+1-x+1=2;
(3)不变,由题意AC=(-1-2t)-(-6-6t)=5+4t,AB=(1+2t)-(-1-2t)=2+4t,
∴AC-AB=(5+4t)-(2+4t)=3,
∴AC-AB的值不变,AC-AB=3.
故答案为:(1)-1;1;-6 (2)2 (3)不变;3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,O在AB上,以O为圆心,OB长为半径的圆与BC交于点D,DE⊥AC于E.
(1)求证:DE是⊙O的切线;
(2)若AC与⊙O相切于F,AB=5,sinA=
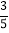 ,求⊙O的半径.
,求⊙O的半径.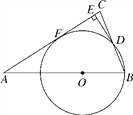
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A=∠BCD=90°,BC=CD,CE⊥AD,垂足为E,求证:AE=CE.
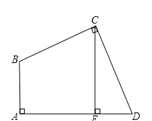
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F

(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是等边三角形,D是BC边上的一个动点
是等边三角形,D是BC边上的一个动点 点D不与B,C重合
点D不与B,C重合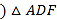 是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF.
是以AD为边的等边三角形,过点F作BC的平行线交射线AC于点E,连接BF. 如图1,求证:
如图1,求证: ≌
≌ ;
;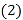 请判断图1中四边形BCEF的形状,并说明理由;
请判断图1中四边形BCEF的形状,并说明理由;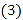 若D点在BC边的延长线上,如图2,其它条件不变,请问
若D点在BC边的延长线上,如图2,其它条件不变,请问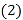 中结论还成立吗?如果成立,请说明理由.
中结论还成立吗?如果成立,请说明理由.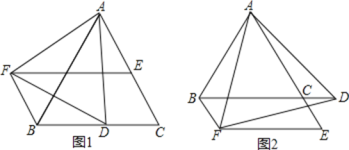
-
科目: 来源: 题型:
查看答案和解析>>【题目】周日上午小明从家跑步去图书馆,在那里看了一会儿书后又走到文具店去买笔记本,然后散步回家.下图反映的是小明离家的距离
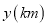 与所用时间
与所用时间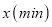 之间的函数关系,据此回答问题:
之间的函数关系,据此回答问题: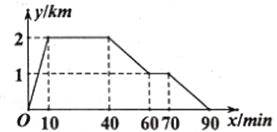
(1)图书馆离小明家
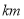 ,小明从家到图书馆用了
,小明从家到图书馆用了 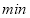 .
.(2)图书馆离文具店____
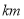 .
.(3)小明在文具店停留了
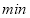
(4)小明从文具店回到家的平均速度是多少千米/小时?(写出简要计算过程)
相关试题

