【题目】某校为了更好地开展球类运动,体育组决定用1600元购进足球8个和篮球14个,并且篮球的单价比足球的单价多20元,请解答下列问题:
(1)求出足球和篮球的单价;
(2)若学校欲用不超过3240元,且不少于3200元再次购进两种球50个,求出有哪几种购买方案?
(3)在(2)的条件下,若已知足球的进价为50元,篮球的进价为65元,则在第二次购买方案中,哪种方案商家获利最多?
参考答案:
【答案】(1)60,80;(2)答案见解析;(3)方案一商家获利最多.
【解析】
(1)设足球的单价为x元,则篮球的单价为(x+20)元,则根据所花的钱数为1600元,可得出方程,解出即可;(2)根据题意所述的不等关系:不超过3240元,且不少于3200元,等量关系:两种球共50个,可得出不等式组,解出即可;(3)分别求出三种方案的利润,继而比较可得出答案.
(1)设足球的单价为x元,则篮球的单价为(x+20)元,
根据题意,得8x+14(x+20)=1600,
解得:x=60,x+20=80.
即足球的单价为60元,则篮球的单价为80元;
(2)设购进足球y个,则购进篮球(50-y)个.
根据题意,得![]() ,
,
解得:![]() ,
,
∵y为整数,
∴y=38,39,40.
当y=38,50-y=12;
当y=39,50-y=11;
当y=40,50-y=10.
故有三种方案:
方案一:购进足球38个,则购进篮球12个;
方案二:购进足球39个,则购进篮球11个;
方案三:购进足球40个,则购进篮球10个;
(3)商家售方案一的利润:38(60-50)+12(80-65)=560(元);
商家售方案二的利润:39(60-50)+11(80-65)=555(元);
商家售方案三的利润:40(60-50)+10(80-65)=550(元).
故第二次购买方案中,方案一商家获利最多.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若n-
 ≤x<n+
≤x<n+ ,则(x)=n.如(0.46)=0,(3.67)=4.给出下列关于(x)的结论:①(1.493)=1;②(2x)=2(x);③若(
,则(x)=n.如(0.46)=0,(3.67)=4.给出下列关于(x)的结论:①(1.493)=1;②(2x)=2(x);③若( x-1)=4,则实数x的取值范围是9≤x<11;④当x≥0时,m为非负整数时,有(m+2017x)=m+(2017x);⑤(x+y)=(x)+(y).其中正确的结论有________________.(填序号)
x-1)=4,则实数x的取值范围是9≤x<11;④当x≥0时,m为非负整数时,有(m+2017x)=m+(2017x);⑤(x+y)=(x)+(y).其中正确的结论有________________.(填序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ACB中,∠C=90°,AC=30cm,BC=25cm,动点P从点C出发,沿CA方向运动,速度是2cm/s,动点Q从点B出发,沿BC方向运动,速度是1cm/s.

(1)几秒后P、Q两点相距25cm?
(2)几秒后△PCQ与△ABC相似?
(3)设△CPQ的面积为S1 , △ABC的面积为S2 , 在运动过程中是否存在某一时刻t,使得S1:S2=2:5?若存在,求出t的值;若不存在,则说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中,有两个不相等实数根的是( )
A.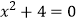
B.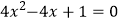
C.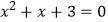
D.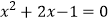
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠α和∠β互补,且∠α>∠β,下列表示角的式子:①90°-∠β;②∠α-90°;③
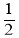 (∠α+∠β);④
(∠α+∠β);④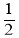 (∠α-∠β).其中能表示∠β的余角的有( )个.
(∠α-∠β).其中能表示∠β的余角的有( )个.A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A.方程x2-4x+2=0无实数根;
B.两条对角线互相垂直且相等的四边形是正方形
C.甲、乙、丙三人站成一排合影留念,则甲、乙二人相邻的概率是
D.若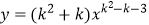 是反比例函数,则k的值为2或-1。
是反比例函数,则k的值为2或-1。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,用火柴棒摆出一列正方形图案,第①个图案用了 4 根,第②个图案用了 12 根,第③个图案用了 24 根,按照这种方式摆下去,摆出第⑥个图案用火柴棒的根数是( )

A. 84 B. 81 C. 78 D. 76
相关试题

