【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线![]() 运动,设运动时间为
运动,设运动时间为![]() 秒。
秒。
(1)AC=______cm;
(2)若点P恰好在∠ABC的角平分线上,求此时![]() 的值;
的值;

参考答案:
【答案】(1)3(2)![]() s.
s.
【解析】
(1)根据题意由勾股定理即可求出AC的长;
(2)点P恰好在∠ABC的角平分线上,设CP=x,根据角平分线的性质得DP=CP=x,BD=BC=4,故AD=1,AP=3-PC=3-x,利用Rt△ADP中AP2=AD2+DP2,即(3-x)2=12+x2,解得x=![]() ,即可求出运动的时间.
,即可求出运动的时间.
(1)根据题意勾股定理即可求出AC=![]()
(2)作DP⊥AB,∵BP为∠ABC的角平分线,
设CP=x,∴DP=CP=x,BD=BC=4,故AD=1,AP=3-PC=3-x,
在Rt△ADP中AP2=AD2+DP2,即(3-x)2=12+x2,
解得x=![]() ,
,
故P点运动的距离为AB+BC+CP=![]()
∴运动的时间为![]() ÷2=
÷2=![]() s.
s.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市预测某饮料有发展前途,用2000元购进一批饮料,面市后果然供不应求,又用5000元购进这批饮料,第二批饮料的数量是第一批的2倍,但进货单价比第一批贵2元.
(1)第一批饮料进货单价多少元?
(2)若二次购进饮料按同一价格销售,两批全部售完后,获利不少2000元,那么销售单价至少为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列文字:
我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式,例如由如图给出了若干个边长为
 和边长为
和边长为 的小正方形纸片及若干个边长为
的小正方形纸片及若干个边长为 的长方形纸片,如图是由如图提供的几何图形拼接而得,可以得到
的长方形纸片,如图是由如图提供的几何图形拼接而得,可以得到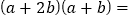

请解答下列问题:
(1)请写出如图中所表示的数学等式:______________________________;
(2)用(1)中所得到的结论,解决下面的问题:已知
 则
则 的值为_________.
的值为_________.(3)①请按要求利用所给的纸片拼出一个长方形,要求所拼出图形的面积为
 并将所拼出的图像画在的方框中;
并将所拼出的图像画在的方框中;②再利用另一种计算面积的方法,可将多项式
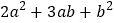 分解因式,即
分解因式,即 _________.
_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取部分学生,就“学习习惯”进行调查,将“对自己做错题进行整理、分析、改正”(选项为:很少、有时、常常、总是)的调查数据进行了整理,绘制成部分统计图如下:

请根据图中信息,解答下列问题:
(1)该调查的样本容量为________,
 =________%,
=________%,  =________%,“常常”对应扇形的圆心角的度数为__________;
=________%,“常常”对应扇形的圆心角的度数为__________;(2)请你补全条形统计图;
(3)若该校有3200名学生,请你估计其中“总是”对错题进行整理、分析、改正的
学生有多少名?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的平面直角坐标系中,一只蚂蚁从A点出发,沿着A-B-C-D-A…循环爬行,其中A点坐标为(1,-1),B点坐标为(-1,-1),C点坐标为(-1,3),D点坐标为(1,3),当蚂蚁爬了2 018个单位长度时,它所处位置的坐标为_____________.
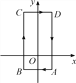
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.

相关试题

