【题目】问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.
小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.
(1)按小明的思路,易求得∠APC的度数为_____度;
(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P在B、D两点之间运动时,问∠APC与α、β之间有何数量关系?请说明理由;
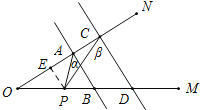
(3)在(2)的条件下,如果点P在B、D两点外侧运动时(点P与点O、B、D三点不重合),请直接写出∠APC与α、β之间的数量关系.

参考答案:
【答案】(1)110°.(2)∠APC=∠α+∠β,(3)当P在BD延长线上时,∠CPA=∠α﹣∠β;当P在DB延长线上时,∠CPA=∠β﹣∠α.
【解析】
试题(1)过点P作PE∥AB,则有PE∥AB∥CD,根据两直线平行,同旁内角互补得到∠A+∠APE=180°,∠C+∠CPE=180°,再根据∠APC=∠APE+∠CPE和已知∠APE和∠CPE度数即可求出∠APC的角度。(2)过P作PE∥AB交AC于E,则有AB∥PE∥CD,进而得到∠α=∠APE,∠β=∠CPE,再根据∠APC=∠APE+∠CPE,即可用α、β来表示∠APC的度数;(3)根据题意画出图形,当P在BD延长线上时,P作PE∥AB交AC于E,则有AB∥PE∥CD,可得到∠CPA=∠β﹣∠α,当如图所示,当P在DB延长线上时,P作PE∥AB交AC于E,则有AB∥PE∥CD,可得到∠CPA=∠β﹣∠α;
试题解析:
(1)解:过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
(2)∠APC=∠α+∠β,
理由:如图2,过P作PE∥AB交AC于E,
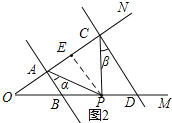
∵AB∥CD,
∴AB∥PE∥CD,
∴∠α=∠APE,∠β=∠CPE,
∴∠APC=∠APE+∠CPE=∠α+∠β;
(3)如图所示,当P在BD延长线上时,
∠CPA=∠α﹣∠β;
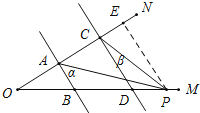
如图所示,当P在DB延长线上时,
∠CPA=∠β﹣∠α.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商场销售A,B两种型号计算器,两种计算器的进货价格分别为每台30元,40元. 商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利120元.
(1)求商场销售A,B两种型号计算器的销售价格分别是多少元?(利润=销售价格﹣进货价格)
(2)商场准备用不多于2500元的资金购进A,B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得
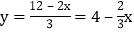 ,(x、y为正整数)∴
,(x、y为正整数)∴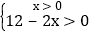 则有0<x<6.又
则有0<x<6.又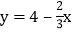 为正整数,则
为正整数,则 为正整数.
为正整数.由2与3互质,可知:x为3的倍数,从而x=3,代入
 .
.∴2x+3y=12的正整数解为

问题:
(1)请你写出方程2x+y=5的一组正整数解:______;
(2)若
 为自然数,则满足条件的x值有______个;
为自然数,则满足条件的x值有______个;A、2B、3C、4D、5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
-
科目: 来源: 题型:
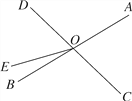
查看答案和解析>>【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分.
(1)图中∠AOC的对顶角为________,∠BOE的补角为________;
(2)若∠AOC=75°,且∠BOE∶∠EOD=1∶4,求∠AOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人共同计算一道整式乘法题:(2x+a)(3x+b).甲由于把第一个多项式中的“+a”看成了“﹣a”,得到的结果为6x2+11x﹣10;乙由于漏抄了第二个多项式中x的系数,得到的结果为2x2﹣9x+10.
(1)求a、b的值.
(2)计算这道乘法题的正确结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为给研究制定《中考改革实施方案》提出合理化建议,教研人员对九年级学生进行了随机抽样调查,要求被抽查的学生从物理、化学、政治、历史、生物和地理这六个选考科目中,挑选出一科作为自己的首选科目,将调查数据汇总整理后,绘制出了如图的两幅不完整的统计图,请你根据图中信息解答下列问题:
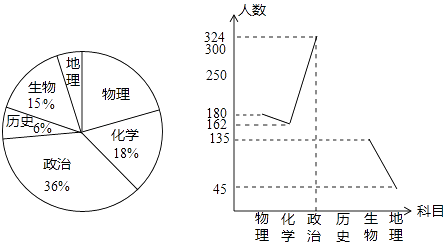
(1)被抽查的学生共有多少人?
(2)将折线统计图补充完整;
(3)我市现有九年级学生约40000人,请你估计首选科目是物理的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线AM∥BN,点E,F,D在射线AM上,点C在射线BN上,且∠BCD=∠A,BE平分∠ABF,BD平分∠FBC.
(1)求证:AB∥CD.
(2)如果平行移动CD,那么∠AFB与∠ADB的比值是否发生变化?若变化,找出变化规律;若不变,求出这两个角的比值.
(3)如果∠A=100°,那么在平行移动CD的过程中,是否存在某一时刻,使∠AEB=∠BDC?若存在,求出此时∠AEB的度数;若不存在,请说明理由.

相关试题

