【题目】定义:有三个内角相等凸四边形叫三等角四边形.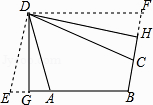
(1)三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;
(2)如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.
(3)三等角四边形ABCD中,∠A=∠B=∠C<90°,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?(作图解答)
参考答案:
【答案】
(1)
解:∵∠A=∠B=∠C,
∴3∠A+∠ADC=360°,
∴∠ADC=360°﹣3∠A.
∵0<∠ADC<180°,
∴0°<360°﹣3∠A<180°,
∴60°<∠A<120°;
(2)
解:证明:∵四边形DEBF为平行四边形,
∴∠E=∠F,且∠E+∠EBF=180°.
∵DE=DA,DF=DC,
∴∠E=∠DAE=∠F=∠DCF,
∵∠DAE+∠DAB=180°,∠DCF+∠DCB=180°,∠E+∠EBF=180°,
∴∠DAB=∠DCB=∠ABC,
∴四边形ABCD是三等角四边形
(3)
解:①当60°<∠A<90°时,如图1,
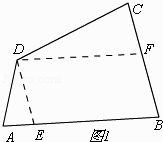
过点D作DF//AB,DE//BC,
∴四边形BEDF是平行四边形,∠DFC=∠B=∠DEA,
∴EB=DF,DE=FB,
∵∠A=∠B=∠C,∠DFC=∠B=∠DEA,
∴△DAE∽△DCF,AD=DE,DC=DF=4,
设AD=x,AB=y,
∴AE=y﹣4,CF=4﹣x,
∵△DAE∽△DCF,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴y=﹣ ![]() x2+x+4=﹣
x2+x+4=﹣ ![]() (x﹣2)2+5,
(x﹣2)2+5,
∴当x=2时,y的最大值是5,
即:当AD=2时,AB的最大值为5,
②当∠A=90°时,三等角四边形是正方形,
∴AD=AB=CD=4,
③当90°<∠A<120°时,∠D为锐角,如图2,
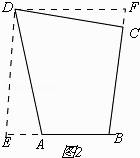
过点D作DE//BC,∠DCB=∠CBA,
∴四边形BCDE是等腰梯形,
∴CD=EB=4,
∵AE=4﹣AB>0,
∴AB<4,
综上所述,当AD=2时,AB的长最大,最大值是5
【解析】(1)根据四边形的内角和是360°,确定出∠A的范围;(2)由四边形DEBF为平行四边形,得到∠E=∠F,且∠E+∠EBF=180°,再根据等角的补角相等,判断出∠DAB=∠DCB=∠ABC,即可;(3)分三种情况分别讨论计算AB的长,从而得出当AD=2时,AB最长;
【考点精析】根据题目的已知条件,利用平行四边形的性质和相似三角形的应用的相关知识可以得到问题的答案,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△AOB中,∠AOB为直角,OA=6,OB=8,半径为2的动圆圆心Q从点O出发,沿着OA方向以1个单位长度/秒的速度匀速运动,同时动点P从点A出发,沿着AB方向也以1个单位长度/秒的速度匀速运动.设运动时间为t秒(0<t≤5)以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为C、D,连结CD、QC.
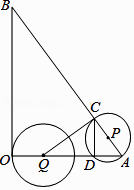
(1)当t为何值时,点Q与点D重合?
(2)当⊙Q经过点A时,求⊙P被OB截得的弦长. -
科目: 来源: 题型:
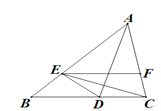
查看答案和解析>>【题目】如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②EC平分∠DEF;③AD垂直平分CE.其中结论正确的有( )个
A. 1 B. 2 C. 3 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,现将△ABC折叠,使点A、B两点重合,折痕所在的直线与直线AC的夹角为40°,则∠B的度数为______°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a+3|与(b+1)2互为相反数,a、b分别对应数轴上的点A、B.
(1)求a、b的值.
(2)数轴上原点右侧存在点C,设甲、乙、丙三个动点分别从A、B、C三点同时运动,甲、乙向数轴正方向运动,丙向数轴负方向运动,甲、乙、丙运动速度分别为1、
 、2(单位长度每秒),若它们在数轴上某处相遇,请求出C点对应的数是多少?
、2(单位长度每秒),若它们在数轴上某处相遇,请求出C点对应的数是多少?(3)运用(2)中所求C点对应的数,若甲、乙、丙出发地及速度大小均不变,同时向数轴负方向运动,问丙先追上谁?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,﹣8),对称轴为x=4.

(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点N以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PN被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点N的运动速度;若不存在,请说明理由;
(3)在(2)的结论下,直线x=1上是否存在点M使△MPN为等腰三角形?若存在,请直接写出所有点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( )

A.1个
B.2个
C.3个
D.4个
相关试题

