【题目】已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,﹣8),对称轴为x=4.
(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点N以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PN被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点N的运动速度;若不存在,请说明理由;
(3)在(2)的结论下,直线x=1上是否存在点M使△MPN为等腰三角形?若存在,请直接写出所有点M的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵抛物线过C(0,﹣8),
∴c=﹣8,即y=ax2+bx﹣8,
由函数经过点(14,0)及对称轴为x=4可得 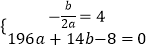 ,
,
解得: 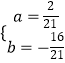 ,
,
∴该抛物线的解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣8
x﹣8
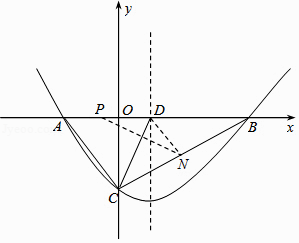
(2)
解:存在直线CD垂直平分PN.
由函数解析式为y= ![]() x2﹣
x2﹣ ![]() x﹣8,可求出点A坐标为(﹣6,0),
x﹣8,可求出点A坐标为(﹣6,0),
在Rt△AOC中,AC= ![]() =
= ![]() =10=AD,
=10=AD,
故可得OD=AD﹣OA=4,点D在函数的对称轴上,
∵线CD垂直平分PN,
∴∠PDC=∠NDC,PD=DN,
由AD=AC可得,∠PDC=∠ACD,
∴∠NDC=∠ACD,
∴DN//AC,
又∵DB=AB﹣AD=20﹣10=10=AD,
∴点D是AB中点,
∴DN为△ABC的中位线,
∴DN= ![]() AC=5,
AC=5,
∴AP=AD﹣PD=AD﹣DN=10﹣5=5,
∴t=5÷1=5(秒),
∴存在t=5(秒)时,线段PN被直线CD垂直平分.
在Rt△BOC中,BC= ![]() =
= ![]() =2
=2 ![]() ,
,
而DN为△ABC的中位线,N是BC中点,
∴CN= ![]() ,
,
∴点N的运动速度为每秒 ![]() 单位长度
单位长度
(3)
解:存在,过点N作NH⊥x轴于H,则NH= ![]() OC=4,
OC=4,
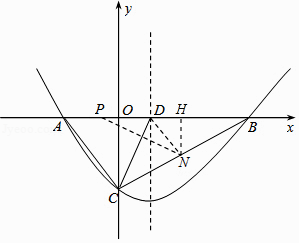
PH=OP+OH=1+7=8,
在Rt△PNH中,PN= ![]() =
= ![]() =4
=4 ![]() ,
,
①当MP=MN,即M为顶点,则此时CD与PN的交点即是M点(上面已经证明CD垂直平分PN),
设直线CD的直线方程为:y=kx+b(k≠0),
因为点C(0,﹣8),点D(4,0),
所以可得直线CD的解析式为:y=2x﹣8,
当x=1时,y=﹣6,
∴M1(1,﹣6);
②当PN为等腰△MPN的腰时,且P为顶点.
设直线x=1上存在点M(1,y),因为点P坐标为(﹣1,0),
从而可得PM2=22+y2,
又PN2=80,
则22+y2=80,
即y=±2 ![]() ,
,
∴M2(1,2 ![]() ),M3(1,﹣2
),M3(1,﹣2 ![]() );
);
③当PN为等腰△MPN的腰时,且N为顶点,点N坐标为(7,﹣4),
设直线x=1存在点M(1,y),
则NM2=62+(y+4)2=80,
解得:y=2 ![]() ﹣4或﹣2
﹣4或﹣2 ![]() ﹣4;
﹣4;
∴M4(1,﹣4+2 ![]() ),M5(1,﹣4﹣2
),M5(1,﹣4﹣2 ![]() ).
).
综上所述:存在这样的五点:M1(1,﹣6),M2(1,2 ![]() ),M3(1,﹣2
),M3(1,﹣2 ![]() ),M4(1,﹣4+2
),M4(1,﹣4+2 ![]() ),M5(1,﹣4﹣2
),M5(1,﹣4﹣2 ![]() ).
).
【解析】(1)由题意抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,﹣8),对称轴为x=4,根据待定系数法可以求得该抛物线的解析式;(2)假设存在,设出时间t,则根据线段PN被直线CD垂直平分,再由垂直平分线的性质及勾股定理来求解t,看t是否存在;(3)假设直线x=1上是存在点M,使△MPN为等腰三角形,此时要分两种情况讨论:①当PN为等腰△MPN的腰时,且P为顶点;②当PN为等腰△MPN的腰时,且Q为顶点;然后再根据等腰三角形的性质及直角三角形的勾股定理求出M点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,现将△ABC折叠,使点A、B两点重合,折痕所在的直线与直线AC的夹角为40°,则∠B的度数为______°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有三个内角相等凸四边形叫三等角四边形.
(1)三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;
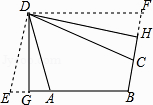
(2)如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.
(3)三等角四边形ABCD中,∠A=∠B=∠C<90°,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?(作图解答) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知|a+3|与(b+1)2互为相反数,a、b分别对应数轴上的点A、B.
(1)求a、b的值.
(2)数轴上原点右侧存在点C,设甲、乙、丙三个动点分别从A、B、C三点同时运动,甲、乙向数轴正方向运动,丙向数轴负方向运动,甲、乙、丙运动速度分别为1、
 、2(单位长度每秒),若它们在数轴上某处相遇,请求出C点对应的数是多少?
、2(单位长度每秒),若它们在数轴上某处相遇,请求出C点对应的数是多少?(3)运用(2)中所求C点对应的数,若甲、乙、丙出发地及速度大小均不变,同时向数轴负方向运动,问丙先追上谁?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中变形正确的是( )
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③
 +
+ =4去分母,得3x+2x=24;
=4去分母,得3x+2x=24;④(x+2)-2(x-1)=0去括号,得x+2-2x-2=0.
A. ①③ B. ①②③ C. ①④ D. ①③④
-
科目: 来源: 题型:
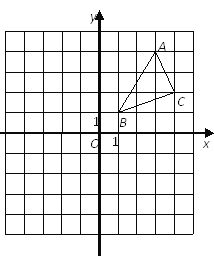
查看答案和解析>>【题目】在如图所示的方格纸中,△ABC的顶点都在小正方形的顶点上,以小正方形互相垂直的两边所在直线建立直角坐标系.
(1)作出△ABC关于y轴对称的△A1B1C1,其中A,B,C分别和A1,B1,C1对应;
(2)平移△ABC,使得A点在x轴上,B点在y轴上,平移后的三角形记为△A2B2C2,作出平移后的△A2B2C2,其中A,B,C分别和A2,B2,C2对应;
(3)△ABC的面积是________.
相关试题

