【题目】已知|a+3|与(b+1)2互为相反数,a、b分别对应数轴上的点A、B.
(1)求a、b的值.
(2)数轴上原点右侧存在点C,设甲、乙、丙三个动点分别从A、B、C三点同时运动,甲、乙向数轴正方向运动,丙向数轴负方向运动,甲、乙、丙运动速度分别为1、![]() 、2(单位长度每秒),若它们在数轴上某处相遇,请求出C点对应的数是多少?
、2(单位长度每秒),若它们在数轴上某处相遇,请求出C点对应的数是多少?
(3)运用(2)中所求C点对应的数,若甲、乙、丙出发地及速度大小均不变,同时向数轴负方向运动,问丙先追上谁?为什么?
参考答案:
【答案】(1)![]() ;(2)5;(3)丙先追上乙.
;(2)5;(3)丙先追上乙.
【解析】
(1)由|a+3|与(b+1)2互为相反数可知|a+3|+(b+1)2=0,根据绝对值和平方的非负数性质即可得答案;(2)设点C对应的数是x,根据题意列出方程,求出方程的解即可得到结果;(3)设丙追上乙所需时间为a秒,丙追上甲所需时间为b秒,分别求出各自的时间,比较即可得到结果.
(1)∵|a+3|与(b+1)2互为相反数,即|a+3|+(b+1)2=0,
∴![]() ,
,
解得:![]() ;
;
(2)设C点对应的数是x,
则甲、丙从出发到相遇所需时间为![]() ,乙、丙从出发到相遇所需时间为
,乙、丙从出发到相遇所需时间为![]() ,
,
∴![]() ,
,
∴x=5;
(3)设丙追上乙所需时间为a秒,丙追上甲所需时间为b秒,
根据题意得:(2﹣![]() )a=5+1,即a=
)a=5+1,即a=![]() ;
;
(2﹣1)b=5+3,即b=8,
∵![]() <8,
<8,
∴丙先追上乙.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是角平分线,E是AB上一点,AE=AC,EF∥BC交AC于F.下列结论①△ADC≌△ADE;②EC平分∠DEF;③AD垂直平分CE.其中结论正确的有( )个
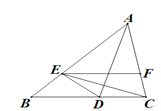
A. 1 B. 2 C. 3 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC,现将△ABC折叠,使点A、B两点重合,折痕所在的直线与直线AC的夹角为40°,则∠B的度数为______°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义:有三个内角相等凸四边形叫三等角四边形.
(1)三等角四边形ABCD中,∠A=∠B=∠C,求∠A的取值范围;
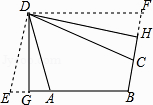
(2)如图,折叠平行四边形纸片DEBF,使顶点E,F分别落在边BE,BF上的点A,C处,折痕分别为DG,DH.求证:四边形ABCD是三等角四边形.
(3)三等角四边形ABCD中,∠A=∠B=∠C<90°,若CB=CD=4,则当AD的长为何值时,AB的长最大,其最大值是多少?(作图解答) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c(a>0)的图象经过点B(14,0)和C(0,﹣8),对称轴为x=4.

(1)求该抛物线的解析式;
(2)点D在线段AB上且AD=AC,若动点P从A出发沿线段AB以每秒1个单位长度的速度匀速运动,同时另一动点N以某一速度从C出发沿线段CB匀速运动,问是否存在某一时刻,使线段PN被直线CD垂直平分?若存在,请求出此时的时间t(秒)和点N的运动速度;若不存在,请说明理由;
(3)在(2)的结论下,直线x=1上是否存在点M使△MPN为等腰三角形?若存在,请直接写出所有点M的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( )

A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程中变形正确的是( )
①3x+6=0变形为x+2=0;
②2x+8=5-3x变形为x=3;
③
 +
+ =4去分母,得3x+2x=24;
=4去分母,得3x+2x=24;④(x+2)-2(x-1)=0去括号,得x+2-2x-2=0.
A. ①③ B. ①②③ C. ①④ D. ①③④
相关试题

