【题目】如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.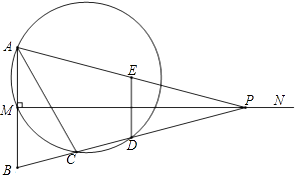
(1)当∠APB=28°时,求∠B和 ![]() 的度数;
的度数;
(2)求证:AC=AB.
(3)在点P的运动过程中
①当MP=4时,取四边形ACDE一边的两端点和线段MP上一点Q,若以这三点为顶点的三角形是直角三角形,且Q为锐角顶点,求所有满足条件的MQ的值;
②记AP与圆的另一个交点为F,将点F绕点D旋转90°得到点G,当点G恰好落在MN上时,连结AG,CG,DG,EG,直接写出△ACG和△DEG的面积之比.
参考答案:
【答案】
(1)
解:∵MN⊥AB,AM=BM,
∴PA=PB,
∴∠PAB=∠B,
∵∠APB=28°,
∴∠B=76°,
如图1,连接MD,

∵MD为△PAB的中位线,
∴MD∥AP,
∴∠MDB=∠APB=28°,
∴ ![]() =2∠MDB=56°;
=2∠MDB=56°;
(2)
证明:∵∠BAC=∠MDC=∠APB,
又∵∠BAP=180°﹣∠APB﹣∠B,∠ACB=180°﹣∠BAC﹣∠B,
∴∠BAP=∠ACB,
∵∠BAP=∠B,
∴∠ACB=∠B,
∴AC=AB;
(3)
解:①如图2,记MP与圆的另一个交点为R,

∵MD是Rt△MBP的中线,
∴DM=DP,
∴∠DPM=∠DMP=∠RCD,
∴RC=RP,
∵∠ACR=∠AMR=90°,
∴AM2+MR2=AR2=AC2+CR2,
∴12+MR2=22+PR2,
∴12+(4﹣PR)2=22+PR2,
∴PR= ![]() ,
,
∴MR= ![]() ,
,
Ⅰ.当∠ACQ=90°时,AQ为圆的直径,
∴Q与R重合,
∴MQ=MR= ![]() ;
;
Ⅱ.如图3,当∠QCD=90°时,

在Rt△QCP中,PQ=2PR= ![]() ,
,
∴MQ= ![]() ;
;
Ⅲ.如图4,当∠QDC=90°时,

∵BM=1,MP=4,
∴BP= ![]() ,
,
∴DP= ![]() BP=
BP= ![]() ,
,
∵cos∠MPB= ![]() =
= ![]() ,
,
∴PQ= ![]() ,
,
∴MQ= ![]() ;
;
Ⅳ.如图5,当∠AEQ=90°时,

由对称性可得∠AEQ=∠BDQ=90°,
∴MQ= ![]() ;
;
综上所述,MQ的值为 ![]() 或
或 ![]() 或
或 ![]() ;
;
②△ACG和△DEG的面积之比为 ![]() .
.
理由:如图6,∵DM∥AF,
∴DF=AM=DE=1,
又由对称性可得GE=GD,
∴△DEG是等边三角形,
∴∠EDF=90°﹣60°=30°,
∴∠DEF=75°=∠MDE,
∴∠GDM=75°﹣60°=15°,
∴∠GMD=∠PGD﹣∠GDM=15°,
∴GMD=∠GDM,
∴GM=GD=1,
过C作CH⊥AB于H,

由∠BAC=30°可得CH= ![]() AC=
AC= ![]() AB=1=MG,AH=
AB=1=MG,AH= ![]() ,
,
∴CG=MH= ![]() ﹣1,
﹣1,
∴S△ACG= ![]() CG×CH=
CG×CH= ![]() ,
,
∵S△DEG= ![]() ,
,
∴S△ACG:S△DEG= ![]() .
.
【解析】(1)根据三角形ABP是等腰三角形,可得∠B的度数,再连接MD,根据MD为△PAB的中位线,可得∠MDB=∠APB=28°,进而得到 ![]() =2∠MDB=56°;(2)根据∠BAP=∠ACB,∠BAP=∠B,即可得到∠ACB=∠B,进而得出AC=AB;(3)①记MP与圆的另一个交点为R,根据AM2+MR2=AR2=AC2+CR2 , 即可得到PR=
=2∠MDB=56°;(2)根据∠BAP=∠ACB,∠BAP=∠B,即可得到∠ACB=∠B,进而得出AC=AB;(3)①记MP与圆的另一个交点为R,根据AM2+MR2=AR2=AC2+CR2 , 即可得到PR= ![]() ,MR=
,MR= ![]() ,再根据Q为直角三角形锐角顶点,分四种情况进行讨论:当∠ACQ=90°时,当∠QCD=90°时,当∠QDC=90°时,当∠AEQ=90°时,即可求得MQ的值为
,再根据Q为直角三角形锐角顶点,分四种情况进行讨论:当∠ACQ=90°时,当∠QCD=90°时,当∠QDC=90°时,当∠AEQ=90°时,即可求得MQ的值为 ![]() 或
或 ![]() 或
或 ![]() ;②先判定△DEG是等边三角形,再根据GMD=∠GDM,得到GM=GD=1,过C作CH⊥AB于H,由∠BAC=30°可得CH=
;②先判定△DEG是等边三角形,再根据GMD=∠GDM,得到GM=GD=1,过C作CH⊥AB于H,由∠BAC=30°可得CH= ![]() AC=1=MG,即可得到CG=MH=
AC=1=MG,即可得到CG=MH= ![]() ﹣1,进而得出S△ACG=
﹣1,进而得出S△ACG= ![]() CG×CH=
CG×CH= ![]() ,再根据S△DEG=
,再根据S△DEG= ![]() ,即可得到△ACG和△DEG的面积之比.
,即可得到△ACG和△DEG的面积之比.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图,请根据统计图表提供的信息解答下列问题:
种类
频数
频率
卡通画
a
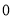 .45
.45时文杂志
b
0.16
武侠小说
50
c
文学名著
d
e
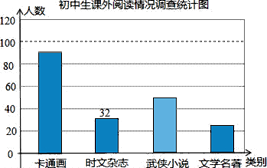
(1)这次随机调查了______名学生,统计表中a=______,d=______;
(2)假如以此统计表绘出扇形统计图,则武侠小说对应的圆心角是______;
(3)试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电子品牌商下设台式电脑部、平板电脑部、手机部等.2018年的前五个月该品牌全部商品销售额共计600万元.下表表示该品牌商2018年前五个月的月销售额(统计信息不全).图1表示该品牌手机部各月销售额占该品牌所有商品当月销售额的百分比情况统计图.
品牌月销售额统计表(单位:万元)
月份
1月
2月
3月
4月
5月
品牌月销售额
180
90
115
95

(
 )该品牌5月份的销售额是 万元;
)该品牌5月份的销售额是 万元;(
 )手机部5月份的销售额是 万元;
)手机部5月份的销售额是 万元;小明同学观察图1后认为,手机部5月份的销售额比手机部4月份的销售额减少了,你同意他的看法吗?请说明理由;
(
 )该品牌手机部有A、B、C、D、E五个机型,图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图.则5月份 机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是 .
)该品牌手机部有A、B、C、D、E五个机型,图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图.则5月份 机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD平分∠ABC. 请补全图形后,依条件完成解答.
(1)在直线BC下方画∠CBE,使∠CBE与∠ABC互补;
(2)在射线BE上任取一点F,过点F画直线FG∥BD交BC于点G;
(3)判断∠BFG与∠BGF的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF.
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将不等式组
 的解集表示在数轴上,下面表示正确的是( )
的解集表示在数轴上,下面表示正确的是( )
A.
B.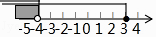
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
相关试题

