【题目】某电子品牌商下设台式电脑部、平板电脑部、手机部等.2018年的前五个月该品牌全部商品销售额共计600万元.下表表示该品牌商2018年前五个月的月销售额(统计信息不全).图1表示该品牌手机部各月销售额占该品牌所有商品当月销售额的百分比情况统计图.
品牌月销售额统计表(单位:万元)
月份 | 1月 | 2月 | 3月 | 4月 | 5月 |
品牌月销售额 | 180 | 90 | 115 | 95 |

(![]() )该品牌5月份的销售额是 万元;
)该品牌5月份的销售额是 万元;
(![]() )手机部5月份的销售额是 万元;
)手机部5月份的销售额是 万元;
小明同学观察图1后认为,手机部5月份的销售额比手机部4月份的销售额减少了,你同意他的看法吗?请说明理由;
(![]() )该品牌手机部有A、B、C、D、E五个机型,图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图.则5月份 机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是 .
)该品牌手机部有A、B、C、D、E五个机型,图2表示在5月份手机部各机型销售额占5月份手机部销售额的百分比情况统计图.则5月份 机型的销售额最高,销售额最高的机型占5月份该品牌销售额的百分比是 .
参考答案:
【答案】(1)120;(2)36.小明说法错误,理由见解析;(3)B,8.4%.
【解析】
(1)由已知的前5月的销售总额为600万元,结合统计表中所给的前4个月的销售额即可求得5月份的销售额;
(2)由(1)中所得5月份的销售额和已知条件计算出4、5两月手机部的销售额即可得到所求答案;
(3)由扇形统计图中的信息可知,5月份手机部销售的手机中B型手机的销售额最高,由(2)中所得5月份手机部的销售额结合扇形统计图中的信息可计算出5月份B型手机的销售额,这样结合(1)中所得5月份该品牌的销售总额即可计算出5月份B型手机的销售额占5月份该品牌销售总额的百分比.
(1)由题意可得:
该品牌5月份的销售额为:600-180-90-115-95=120(万元);
(2)由题意可得:
手机部5月份的销售额为:120×30%=36(万元);
不同意小明的看法,理由如下:
由题意可得:手机部4月份销售额为:95×32%=30.4(万元),手机部5月份销售额为:120×30%=36(万元),
∵36万元>30.4万元,
∴小明的说法错误;
(3)由扇形统计图可知,5月份手机部销售的手机中B型手机的销售额最高;
由(2)可知5月份手机部销售手机的总金额为36万元,其中B型手机占28%,
∴5月份手机部销售B型手机的金额为:36×28%=10.08(万元),
又∵5月份该品牌产品的销售总额为120万元,
∴5月份B型手机的销售额占该月销售总额的百分比为:10.08÷120×100%=8.4%.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上, 老师要求同学们利用三角板画两条平行线.老师说苗苗和小华两位同学画法都是正确的,两位同学的画法如下:
苗苗的画法:

①将含30°角的三角尺的最长边与直线a重合,另一块三角尺最长边与含30°角的三角尺的最短边紧贴;
②将含30°角的三角尺沿贴合边平移一段距离,画出最长边所在直线b,则b//a.
小华的画法:
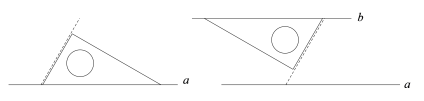
①将含30°角三角尺的最长边与直线a重合,用虚线做出一条最短边所在直线;
②再次将含30°角三角尺的最短边与虚线重合,画出最长边所在直线b,则b//a.
请在苗苗和小华两位同学画平行线的方法中选出你喜欢的一种,并写出这种画图的依据.
答:我喜欢__________同学的画法,画图的依据是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为创建大数据应用示范城市,我市某机构针对市民最关心的四类生活信息进行了民意调查(被调查者每人限选一项),下面是部分四类生活信息关注度统计图表,请根据图中提供的信息解答下列问题:
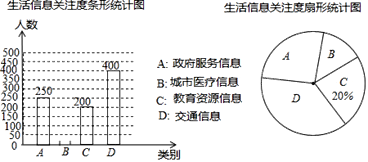
(1)本次参与调查的人数有______ 人;
(2)关注城市医疗信息的有______ 人,并补全条形统计图;
(3)扇形统计图中,D部分的圆心角是______度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图,请根据统计图表提供的信息解答下列问题:
种类
频数
频率
卡通画
a
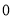 .45
.45时文杂志
b
0.16
武侠小说
50
c
文学名著
d
e
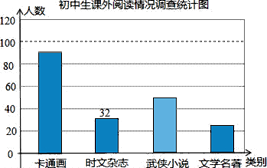
(1)这次随机调查了______名学生,统计表中a=______,d=______;
(2)假如以此统计表绘出扇形统计图,则武侠小说对应的圆心角是______;
(3)试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知BD平分∠ABC. 请补全图形后,依条件完成解答.
(1)在直线BC下方画∠CBE,使∠CBE与∠ABC互补;
(2)在射线BE上任取一点F,过点F画直线FG∥BD交BC于点G;
(3)判断∠BFG与∠BGF的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.
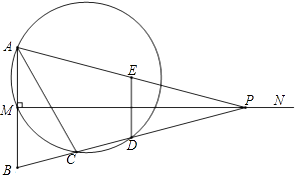
(1)当∠APB=28°时,求∠B和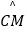 的度数;
的度数;
(2)求证:AC=AB.
(3)在点P的运动过程中
①当MP=4时,取四边形ACDE一边的两端点和线段MP上一点Q,若以这三点为顶点的三角形是直角三角形,且Q为锐角顶点,求所有满足条件的MQ的值;
②记AP与圆的另一个交点为F,将点F绕点D旋转90°得到点G,当点G恰好落在MN上时,连结AG,CG,DG,EG,直接写出△ACG和△DEG的面积之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF.
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.

相关试题

