【题目】某小区准备新建50个停车位,用以解决小区停车难的问题.已知新建1个地上停车位和1个地下停车位共需0.6万元;新建3个地上停车位和2个地下停车位共需1.3万元.
(1)该小区新建1个地上停车位和1个地下停车位各需多少万元?
(2)该小区的物业部门预计投资金额超过12万元而不超过13万元,那么共有几种建造停车位的方案?
参考答案:
【答案】(1)0.1,0.5;(2)3.
【解析】
试题(1)先设该小区新建1个地上停车位需要x万元,1个地下停车位需y万元,再根据新建1个地上停车位和1个地下停车位需0.6万元,新建,3个地上停车位和2个地下停车位需1.3万元,列出方程组进行求解即可;
(2)先设出新建a个地上停车位,再根据投资金额超过10万元而不超过13万元,列出不等式即可得出建造方案.
试题解析:设该小区新建1个地上停车位需要x万元,1个地下停车位需y万元,根据题意得:![]() ,解得:
,解得:![]() .故该小区新建1个地上停车位需要0.1万元,1个地下停车位需0.4万元.
.故该小区新建1个地上停车位需要0.1万元,1个地下停车位需0.4万元.
(2)设新建a个地上停车位,根据题意得:![]() ,解得:
,解得:![]() ,根据题意因为a只能取整数,所以a=30或a=31或a=32,对应的50﹣a=50﹣30=20或50﹣31=19或50﹣32=18,所以则共有3种建造方案.
,根据题意因为a只能取整数,所以a=30或a=31或a=32,对应的50﹣a=50﹣30=20或50﹣31=19或50﹣32=18,所以则共有3种建造方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB=2,MN⊥AB于点M,且AM=BM,P是射线MN上一动点,E,D分别是PA,PB的中点,过点A,M,D的圆与BP的另一交点C(点C在线段BD上),连结AC,DE.
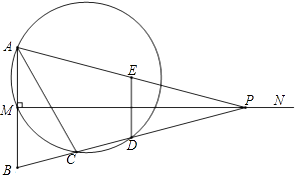
(1)当∠APB=28°时,求∠B和 的度数;
的度数;
(2)求证:AC=AB.
(3)在点P的运动过程中
①当MP=4时,取四边形ACDE一边的两端点和线段MP上一点Q,若以这三点为顶点的三角形是直角三角形,且Q为锐角顶点,求所有满足条件的MQ的值;
②记AP与圆的另一个交点为F,将点F绕点D旋转90°得到点G,当点G恰好落在MN上时,连结AG,CG,DG,EG,直接写出△ACG和△DEG的面积之比. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD和四边形DEFG都是正方形,点E,G分别在AD,CD上,连接AF,BF,CF.
(1)求证:AF=CF;
(2)若∠BAF=35°,求∠BFC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将不等式组
 的解集表示在数轴上,下面表示正确的是( )
的解集表示在数轴上,下面表示正确的是( )
A.
B.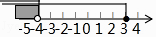
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在□ABCD中,AC为对角线,AC=BC=5,AB=6,AE是△ABC的中线,求△ACE的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数
 ,导致了第一次数学危机,
,导致了第一次数学危机,  是无理数的证明如下: 假设
是无理数的证明如下: 假设  是有理数,那么它可以表示成
是有理数,那么它可以表示成  (p与q是互质的两个正整数).于是(
(p与q是互质的两个正整数).于是(  )2=(
)2=(  )2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“
)2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“  是有理数”的假设不成立,所以,
是有理数”的假设不成立,所以,  是无理数.
是无理数.
这种证明“ 是无理数”的方法是( )
是无理数”的方法是( )
A.综合法
B.反证法
C.举反例法
D.数学归纳法 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )

A.5πcm2
B.10πcm2
C.15πcm2
D.20πcm2
相关试题

