【题目】已知函数y=(2m+1)x+m﹣3,
(1)若函数图像经过原点,求m的值;
(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
参考答案:
【答案】
(1)解:把(0,0)代入,得:m﹣3=0,m=3
(2)解:根据y随x的增大而减小说明k<0.即2m+1<0.
解得:m< ![]()
【解析】(1)根据待定系数法,只需把原点代入即可求解;(2)直线y=kx+b中,y随x的增大而减小说明k<0.
【考点精析】认真审题,首先需要了解一次函数的性质(一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小),还要掌握确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在△ABC中,∠A:∠B:∠C=2:3:4,CD是∠ACB平分线,求∠A和∠CDB的度数.

-
科目: 来源: 题型:
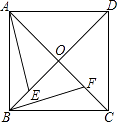
查看答案和解析>>【题目】如图,在正方形ABCD中,OE=OF.求证:△AOE≌△BOF,AE⊥BF.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90o,AB=AD,AE=AC, AF⊥CF,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;
(3)求证:CE=2AF .

-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于
 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,E、F是对角线BD上的两点,且BE=DF. 求证:
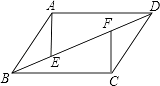
(1)AE=CF;
(2)AE∥CF.
相关试题

