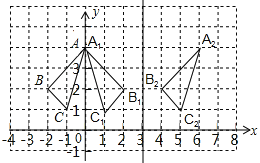
【题目】△ABC在平面直角坐标系中的位置如图所示.
(1)作出△ABC关于![]() 轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;
(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;
(3)观察△A1B1C和△A2B2C2,它们是否关于某直线对称?若是,请用实线条画出对称轴。

参考答案:
【答案】(1)如图,△A1B1C1即为所求,顶点C1的坐标为(1,1);
(2)如图,△A2B2C2即为所求,顶点C2的坐标为(5,1);
(3)△A1B1C1和△A2B2C2关于直线x=3对称如图:
【解析】
试题(1)根据轴对称的性质作出A、B、C关于y轴的对称点,A1、B1、C1,顺次连接画图,并找到坐标即可.(2)根据平移的性质将A、B、C按平移条件找出它的对应点A2、B2、C2,顺次连接画图,并找坐标即可.(3)观察图象即可得△A1B1C1和△A2B2C2,关于直线x=3对称.
试题解析:(1)如图,各顶点的坐标为:A1(0,4) B1 (2,2) C1(1,1);
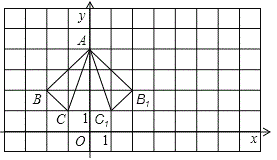
(2)如图,各顶点的坐标为:A2 (6,4) B2 (4,2) C2(5,1);
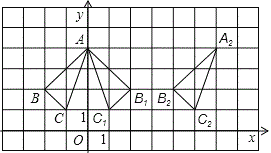
(3)是关于某直线对称,对称轴是直线x=3.如图.
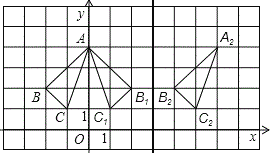
-
科目: 来源: 题型:
查看答案和解析>>【题目】某农场去年计划生产玉米和小麦共200吨.采用新技术后,实际产量为225吨,其中玉米超产5%,小麦超产15%.该农场去年实际生产玉米、小麦各多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y=(2m+1)x+m﹣3,
(1)若函数图像经过原点,求m的值;
(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAD=∠CAE=90o,AB=AD,AE=AC, AF⊥CF,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;
(3)求证:CE=2AF .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平行四边形ABCD中,E、F是对角线BD上的两点,且BE=DF. 求证:
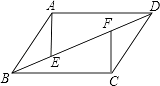
(1)AE=CF;
(2)AE∥CF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l1对应的函数表达式为y=2x-2,直线l1与x轴交于点D.直线l2:y=kx+b与x轴交于点A,且经过点B,直线l1,l2交于点C(m,2).
(1)求点D,点C的坐标;
(2)求直线l2对应的函数表达式;
(3)求△ADC的面积;
(4)利用函数图象写出关于x,y的二元一次方程组
 的解.
的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】校田园科技社团计划购进A,B两种花卉,两次购买每种花卉的数量以及每次的总费用如下表所示:
花卉数量(单位:株)
总费用
(单位:元)
A
B
第一次购买
10
25
225
第二次购买
20
15
275
(1)你从表格中获取了什么信息?______________________________(请用自己的语言描述,写出一条即可);
(2)A,B两种花卉每株的价格各是多少元?
相关试题

