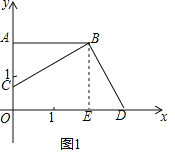
【题目】如图,在平面直角坐标系xOy中,点A在y轴上,点B是第一象限的点,且AB⊥y轴,且AB=OA,点C是线段OA上任意一点,连接BC,作BD⊥BC,交x轴于点D.
(1)依题意补全下图;
(2)用等式表示线段OA,AC与OD之间的数量关系,并证明;
(3)连接CD,作∠CBD的平分线,交CD边于点H,连接AH,求∠BAH的度数.

参考答案:
【答案】(1)见解析;(2)OA+AC=OD,见解析;(3)45°
【解析】
(1)根据题意画出图形即可;
(2)过B作BE⊥x轴于E,则四边形AOEB是矩形,根据矩形的想知道的BE=AO,∠ABE=90°,等量代换得到AB=BE推出△ABC≌△EBD,根据全等三角形的性质得到AC=DE,等量代换即可得到结论;
(3)根据全等三角形的性质得到BC=BD,推出△BCD是等腰直角三角形,于是得到∠BCD=45°,根据等腰三角形的性质得到∠BHC=90°,过H作HN⊥OA,HM⊥AB,证明△CNH≌△BHM,可得出HN=HM,则AH平分∠CAB,可得到结论.
解:(1)如图1所示,
(2)OA+AC=OD,
如图1,过B作BE⊥x轴于E,
则四边形AOEB是矩形,
∴BE=AO,∠ABE=90°,
∵AB=AO,
∴AB=BE,
∵BD⊥BC,
∴∠CBD=90°,
∴∠ABC=∠DBE,
在△ABC与△BDE中,
 ,
,
∴△ABC≌△EBD(ASA),
∴AC=DE,
∵OE=AB=OA,
∴AO+AC=OD;
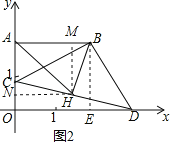
(3)如图2,由(1)知:△ABC≌△EBD,
∴BC=BD,
∵BD⊥BC,
∴△BCD是等腰直角三角形,
∴∠BCD=45°,
∵BH平分∠CBD,
∴∠BHC=90°,
∵∠BAO=90°,
过H作HN⊥OA,HM⊥AB,
∴四边形ANMH是矩形,
∴∠NHM=90°,
∴∠NHC=∠MHB,
∴△CNH≌△BHM(AAS),
∴HN=HM,
∴AH平分∠CAB,
∴∠BAH=45°.
-
科目: 来源: 题型:
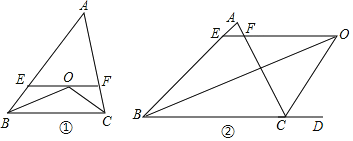
查看答案和解析>>【题目】(1)如图①,△ABC中,∠ABC、∠ACB的平分线交于O点,过O点作EF∥BC交AB、AC于点E、F,试猜想EF、BE、CF之间有怎样的关系,并说明理由;
(2)如图,若将图①中∠ACB的平分线改为外角∠ACD的平分线,其它条件不变,请直接写出EF、BE、CF之间的关系 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】吉祥超市准备购进甲、乙两种绿色袋装食品共800袋.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲
乙
进价(元/袋)
m
m﹣2
售价(元/袋)
20
13
(1)求m的值;
(2)假如购进的甲、乙两种绿色袋装食品全部卖出,所获总利润不少于5200元,且不超过5280元,问该超市有几种进货方案?(利润=售价﹣进价)
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探究)如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示),通过观察比较图2与图1中的阴影部分面积,可以得到乘法公式 .(用含a,b的等式表示)
(应用)请应用这个公式完成下列各题:
(1)已知4m2=12+n2,2m+n=4,则2m﹣n的值为 .
(2)计算:20192﹣2020×2018.
(拓展)计算:1002﹣992+982﹣972+…+42﹣32+22﹣12.

-
科目: 来源: 题型:
查看答案和解析>>【题目】北京世界园艺博览会(简称“世园会”)园区2019年4月29日至2019年10月7日在中国北京市延庆区举行,门票价格如表:小明全家于9月28日集体入园参观游览,通过计算发现:若提前两天线上购买门票所需费用为996元,而入园当天购票所需费用为1080元,则该家庭中可以购买优惠票的有_____人.
票种
票价(元/人)
指定日
普通票
160
优惠票
100
平日
普通票
120
优惠票
80
注1:“指定日”为开园日(4月29日)、五一劳动节(5月1日)、端午节、中秋节、十一假期(含闭园日),“平日”为世园会会期除“指定日”外的其他日期;
注2:六十周岁及以上老人、十八周岁以下的学生均可购买优惠票;
注3:提前两天及以上线上购买世园会门票,票价可打九折,但仅限于普通票.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在圆心角为90°的扇形OAB中,半径OA=2cm,C为
 的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为_____cm2.
的中点,D、E分别是OA、OB的中点,则图中阴影部分的面积为_____cm2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:10月1日,正值祖国母亲70岁生日,我校两校区共有4名教师光荣地加入了群众游行﹣﹣“扬帆远航”方阵;一名老师作为志愿者,负责广场人员的集结和疏散.老师们在周一国旗下讲话时说:“我们的步数、欢呼声、气球浪和笑容都是有指标的”确保队伍行进时做到万无一失.载有国之重器的装甲车,在阅兵时更是精确到秒.从东华表至西华表(东、西华表间的距离为96米)所用的时间是固定的:每辆装甲车必须保证36s之内通过.如果彩排时有两辆装甲车同时从东华表出发,乙的速度是甲的1.1倍,又已知乙到达西华表的时间正好比甲提前3s,那么
(1)甲的速度是每秒多少米(结果精确到1米/秒)?
(2)这两辆装甲车能顺利完成彩排任务吗?请说明理由.

相关试题

