搜索
【题目】吉祥超市准备购进甲、乙两种绿色袋装食品共800袋．甲、乙两种绿色袋装食品的进价和售价如表．已知：用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同．
甲 | 乙 | |
进价（元/袋） | m | m﹣2 |
售价（元/袋） | 20 | 13 |
（1）求m的值；
（2）假如购进的甲、乙两种绿色袋装食品全部卖出，所获总利润不少于5200元，且不超过5280元，问该超市有几种进货方案？（利润＝售价﹣进价）
参考答案：
【答案】（1）10；（2）超市有17种进货方案
【解析】
（1）根据数量＝总价÷单价结合用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同，即可得出关于m的分式方程，解之经检验后即可得出结论；
（2）设购进甲种袋装食品x袋，则购进乙种袋装食品（800﹣x）袋，根据总利润＝每袋的利润×购进数量结合所获总利润不少于5200元且不超过5280元，即可得出关于x的一元一次不等式组，解之即可得出x的取值范围，结合x为正整数即可得出该超市有17种进货方案．
（1）依题意，得： 
，
解得：m＝10，
经检验，m＝10是原方程的解，且符合题意．
答：m的值为10．
（2）设购进甲种袋装食品x袋，则购进乙种袋装食品（800﹣x）袋，
依题意，得：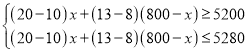
，
解得：240≤x≤256．
∵x为正整数，
∴x＝240，241，242，243，244，245，246，247，248，249，250，251，252，253，254，255，256．
答：该超市有17种进货方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如下图，在平面直角坐标系中，对
进行循环往复的轴对称变换，若原来点A坐标是
，则经过第2019次变换后所得的A点坐标是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知AB为⊙O的直径，AB=2，AD和BE是圆O的两条切线，A、B为切点，过圆上一点C作⊙O的切线CF，分别交AD、BE于点M、N，连接AC、CB，若∠ABC=30°，则AM= ．
-
科目： 来源： 题型：
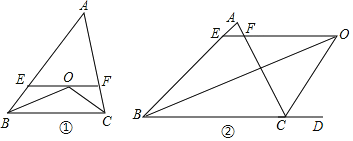
查看答案和解析>>【题目】（1）如图①，△ABC中，∠ABC、∠ACB的平分线交于O点，过O点作EF∥BC交AB、AC于点E、F，试猜想EF、BE、CF之间有怎样的关系，并说明理由；
（2）如图，若将图①中∠ACB的平分线改为外角∠ACD的平分线，其它条件不变，请直接写出EF、BE、CF之间的关系 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（探究）如图1，边长为a的大正方形中有一个边长为b的小正方形，把图1中的阴影部分拼成一个长方形（如图2所示），通过观察比较图2与图1中的阴影部分面积，可以得到乘法公式 ．（用含a，b的等式表示）
（应用）请应用这个公式完成下列各题：
（1）已知4m2＝12+n2，2m+n＝4，则2m﹣n的值为 ．
（2）计算：20192﹣2020×2018．
（拓展）计算：1002﹣992+982﹣972+…+42﹣32+22﹣12．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系xOy中，点A在y轴上，点B是第一象限的点，且AB⊥y轴，且AB＝OA，点C是线段OA上任意一点，连接BC，作BD⊥BC，交x轴于点D．
（1）依题意补全下图；
（2）用等式表示线段OA，AC与OD之间的数量关系，并证明；
（3）连接CD，作∠CBD的平分线，交CD边于点H，连接AH，求∠BAH的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】北京世界园艺博览会（简称“世园会”）园区2019年4月29日至2019年10月7日在中国北京市延庆区举行，门票价格如表：小明全家于9月28日集体入园参观游览，通过计算发现：若提前两天线上购买门票所需费用为996元，而入园当天购票所需费用为1080元，则该家庭中可以购买优惠票的有_____人．
票种
票价（元/人）
指定日
普通票
160
优惠票
100
平日
普通票
120
优惠票
80
注1：“指定日”为开园日（4月29日）、五一劳动节（5月1日）、端午节、中秋节、十一假期（含闭园日），“平日”为世园会会期除“指定日”外的其他日期；
注2：六十周岁及以上老人、十八周岁以下的学生均可购买优惠票；
注3：提前两天及以上线上购买世园会门票，票价可打九折，但仅限于普通票．
相关试题
