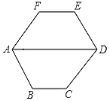
【题目】如图,六边形ABCDEF的内角都相等,∠FAD=60°.
(1)求∠ADE的度数;
(2)求证:EF∥BC.
参考答案:
【答案】(1)∠ADE=60°;(2)详见解析.
【解析】
(1)由于六边形的内角和为720°,然后利用六边形ABCDEF的内角都相等得到每个内角的度数为120°,而∠DAB=60°,四边形ABCD的内角和为360°,由此即可分别求出∠CDA和∠EDA,最后利用平行线的判定方法即可推知AB∥DE,根据平行线的性质即可得到结论;
(2)根据平行线的判定即可得到结论.
(1)∵六边形ABCDEF的内角都相等,
∴∠BAF=∠B=∠C=∠CDE=∠E=∠F=120°,
∵∠FAD=60°,
∴∠F+∠FAD=180°,
∴EF∥AD,
∴∠E+∠ADE=180°,
∴∠ADE=60°;
(2)∵∠BAD=∠FAB﹣∠FAD=60°,
∴∠BAD+∠B=180°,
∴AD∥BC,
∴EF∥BC.
-
科目: 来源: 题型:
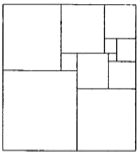
查看答案和解析>>【题目】如图,将一个正方形分割成11个大小不同的正方形,记图中最大正方形的周长是
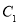 ,最小正方形的周长是
,最小正方形的周长是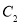 ,则
,则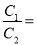 _____.
_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC与BD相交于点O,AB∥CD,AB=CD,则图中的全等三角形共有( )
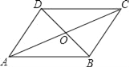
A. 1对B. 2对C. 3对D. 4对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的等边△ABC中,D是BC的中点,点E在线段AD上,连结BE,在BE的下方作等边△BEF,连结DF.当△BDF的周长最小时,∠DBF的度数是_____.
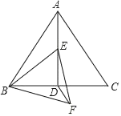
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将矩形OABC置于平面直角坐标系中,点A,C分别在x,y轴的正半轴上,已知点B(4,2),将矩形OABC翻折,使得点C的对应点P恰好落在线段OA(包括端点O,A)上,折痕所在直线分别交BC、OA于点D、E;若点P在线段OA上运动时,过点P作OA的垂线交折痕所在直线于点 Q.设点Q的坐标为(x,y),则y关于x的函数关系式是 .
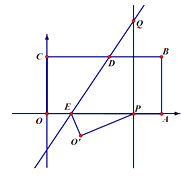
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x,y的方程满足方程组
 .
.(1)若x﹣y=2,求m的值;
(2)若x,y,m均为非负数,求m的取值范围,并化简式子|m﹣3|+|m﹣4|;
(3)在(2)的条件下求s=2x﹣3y+m的最小值及最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个小组同时从山脚开始攀登一座600m高的山,第一小组的攀登速度(即攀登高度与攀登时间之比)是第二小组的1.2倍,并比第二小组早20min到达山顶.
(1)第二小组的攀登速度是多少?
(2)如果山高为hm,第一小组的攀登速度是第二小组的k(k>1)倍,并比第二小组早tmin到达山顶,则第一小组的攀登速度是多少?
相关试题

