【题目】一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮,球沿一条抛物线运动,当球运动的水平距离为2.5m时,达到最大高度3.5m,然后准确落入篮框内.已知篮圈中心距离地面高度为3.05m,在如图所示的平面直角坐标系中,下列说法正确的是( )

A. 此抛物线的解析式是y=﹣![]() x2+3.5
x2+3.5
B. 篮圈中心的坐标是(4,3.05)
C. 此抛物线的顶点坐标是(3.5,0)
D. 篮球出手时离地面的高度是2m
参考答案:
【答案】A
【解析】
A、设抛物线的表达式为y=ax2+3.5,依题意可知图象经过的坐标,由此可得a的值;B、根据函数图象判断;C、根据函数图象判断;D、设这次跳投时,球出手处离地面hm,因为(1)中求得y=﹣0.2x2+3.5,当x=﹣2,5时,即可求得结论.
解:A、∵抛物线的顶点坐标为(0,3.5),
∴可设抛物线的函数关系式为y=ax2+3.5.
∵篮圈中心(1.5,3.05)在抛物线上,将它的坐标代入上式,得 3.05=a×1.52+3.5,
∴a=﹣![]() ,
,
∴y=﹣![]() x2+3.5.
x2+3.5.
故本选项正确;
B、由图示知,篮圈中心的坐标是(1.5,3.05),
故本选项错误;
C、由图示知,此抛物线的顶点坐标是(0,3.5),
故本选项错误;
D、设这次跳投时,球出手处离地面hm,
因为(1)中求得y=﹣0.2x2+3.5,
∴当x=﹣2.5时,
h=﹣0.2×(﹣2.5)2+3.5=2.25m.
∴这次跳投时,球出手处离地面2.25m.
故本选项错误.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=
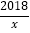 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以等边三角形ABC的BC边为直径画半圆,分别交AB、AC于点E、D,DF是圆的切线,过点F作BC的垂线交BC于点G.若AF的长为2,则FG的长为

A. 4 B.
 C. 6 D.
C. 6 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线
 与
与 轴,
轴, 轴分别交于
轴分别交于 ,
, 两点.直线
两点.直线 与
与 交于点
交于点 且与
且与 轴,
轴, 轴分别交于
轴分别交于 ,
, .
.


图1 图2 图3
(1)求出点
 坐标,直线
坐标,直线 解析式;
解析式;(2)如图2,点
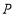 为线段
为线段 上一点(不含端点),连接
上一点(不含端点),连接 ,一动点
,一动点 从
从 出发,沿线段
出发,沿线段 以每秒
以每秒 个单位的速度运动到点
个单位的速度运动到点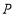 ,再沿线段
,再沿线段 以每秒
以每秒 个单位的速度运动到点
个单位的速度运动到点 停止,求点
停止,求点 在整个运动过程中所用最少时间时点
在整个运动过程中所用最少时间时点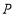 的坐标;
的坐标;(3)如图3,平面直角坐标系中有一点
 ,使得
,使得 ,求点
,求点 坐标.
坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=60°,点D、E分别为边BC、AC上的点,连接DE,过点E作EF∥BC交AB于F,若BC=CE,CD=6,AE=8,∠EDB=2∠A,则BC=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,∠1=∠2,AE⊥OB于E,BD⊥OA于D,交点为C,则图中全等三角形共有( )

A. 2对 B. 3对 C. 4对 D. 5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )

A.①②③B.①③④C.①②④D.①②③④
相关试题

