【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )

A.①②③B.①③④C.①②④D.①②③④
参考答案:
【答案】D
【解析】
根据SAS证△ABD≌△EBC,可得∠BCE=∠BDA,结合∠BCD=∠BDC可得①②正确;根据角的和差以及三角形外角的性质可得∠DCE=∠DAE,即AE=EC,由AD=EC,即可得③正确;过E作EG⊥BC于G点,证明Rt△BEG≌Rt△BEF和Rt△CEG≌Rt△AEF,得到BG=BF和AF=CG,利用线段和差即可得到④正确.
解:①∵BD为△ABC的角平分线,
∴∠ABD=∠CBD,
∴在△ABD和△EBC中,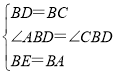 ,
,
∴△ABD≌△EBC(SAS),①正确;
②∵BD为△ABC的角平分线,BD=BC,BE=BA,
∴∠BCD=∠BDC=∠BAE=∠BEA,
∵△ABD≌△EBC,
∴∠BCE=∠BDA,
∴∠BCE+∠BCD=∠BDA+∠BDC=180°,②正确;
③∵∠BCE=∠BDA,∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∠BCD=∠BEA,
∴∠DCE=∠DAE,
∴△ACE为等腰三角形,
∴AE=EC,
∵△ABD≌△EBC,
∴AD=EC,
∴AD=AE=EC.③正确;
④过E作EG⊥BC于G点,
∵E是∠ABC的角平分线BD上的点,且EF⊥AB,
∴EF=EG(角平分线上的点到角的两边的距离相等),
∵在Rt△BEG和Rt△BEF中,![]() ,
,
∴Rt△BEG≌Rt△BEF(HL),
∴BG=BF,
∵在Rt△CEG和Rt△AFE中,![]() ,
,
∴Rt△CEG≌Rt△AEF(HL),
∴AF=CG,
∴BA+BC=BF+FA+BGCG=BF+BG=2BF,④正确.
故选D.
-
科目: 来源: 题型:
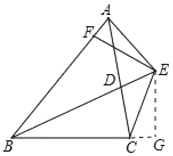
查看答案和解析>>【题目】已知直线AB∥CD,直线EF分别交AB、CD于A、C,CM是∠ACD的平分线,CM交AB于H,过A作AG⊥AC交CM于G.
(1)如图1,点G在CH的延长线上时,
①若∠GAB=36°,则∠MCD=______.
②猜想:∠GAB与∠MCD之间的数量关系是______.
(2)如图2,点G在CH上时,(1)②猜想的∠GAB与∠MCD之间的数量关系还成立吗?如果成立,请给出证明;如果不成立,请写出∠GAB与∠MCD之间的数量关系,并说明理由.
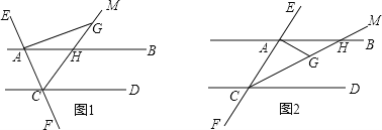
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着“一带一路”国际合作高峰论坛在北京举行,中国同30多个国家签署经贸合作协议,某厂准备生产甲、乙两种商品共8万件销往“一带一路”沿线国家和地区.已知甲种商品的销售单价为900元,乙种商品的销售单价为600元.
(1)已知乙种商品的销售量不能低于甲种商品销售量的三分之一,则最多能销售甲种商品多少万件?
(2)在(1)的条件下,要使甲、乙两种商品的销售总收入不低于5700万元,请求甲种商品销售量的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正方形ABCD,点P是对角线AC所在直线上的动点,点E在BC边所在直线上, PE=PB.
(1)如图1,当点E在线段BC上时,
求证:①PE=PD,②PE⊥PD.
简析: 由正方形的性质,图1中有三对全等的三角形,
即△ABC≌△ADC,_______≌_______,和_______≌______,由全等三角形性质,结合条件中PE=PB,易证PE=PD.要证PE⊥PD,考虑到∠ECD = 90°,故在四边形PECD中,只需证∠PDC +∠PEC=______即可.再结合全等三角形和等腰三角形PBE的性质,结论可证.

(2)如图2,当点E在线段BC的延长线上时,(1)中的结论是否成立?如果成立,请给出证明;如果不成立,请说明理由;

(3)若AB=1,当△PBE是等边三角形时,请直接写出PB的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(知识生成)
我们已经知道,通过不同的方法表示同一图形的面积,可以探求相应的等式.
2002年8月在北京召开了国际数学大会,大会会标如图1所示,它是由四个形状大小完全相同的直角三角形与中间的小正方形拼成的一个大正方形,直角三角形的两条直角边长分别为a、b ( a<b ),斜边长为c.
(1)图中阴影部分的面积用两种方法可分别表示为 、 ;
(2)你能得出的a,b,c之间的数量关系是 (等号两边需化为最简形式);
(3)一直角三角形的两条直角边长为6和8,则其斜边长为 .
(知识迁移)
通过不同的方法表示同一几何体的体积,也可以探求相应的等式.如图2是边长为a+b的正方体,被如图所示的分割线分成8块.
(4)用不同方法计算这个正方体体积,就可以得到一个等式,这个等式可以为 .(等号两边需化为最简形式)
(5)已知a+b=3,ab=1,利用上面的规律求a3+b3的值.
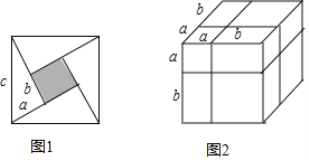
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点
 若点D为BC边的中点,点M为线段EF上一动点,则
若点D为BC边的中点,点M为线段EF上一动点,则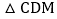 周长的最小值为
周长的最小值为

A. 6 B. 8 C. 10 D. 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C,点D是该抛物线的顶点.
(1)求抛物线的解析式和直线AC的解析式;
(2)请在y轴上找一点M,使△BDM的周长最小,求出点M的坐标;
(3)试探究:在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.

相关试题

