搜索
【题目】如图，在△ABC中，∠C=60°，点D、E分别为边BC、AC上的点，连接DE，过点E作EF∥BC交AB于F，若BC=CE，CD=6，AE=8，∠EDB=2∠A，则BC=_____．
参考答案：
【答案】16
【解析】
利用∠EDB=2∠A作辅助线，求出DE即可.
连接BE，延长BC使CG=AE，连接EG.因为BC=CE，∠ACB=60°，所以△BEC为等边三角形，且EF∥BC，所以∠EBC=∠BEC=∠FEB=∠AEF=∠ACB=60°.因为EC=BE，CG=AE，∠AEB=∠ECG=120°，所以△AEB≌△GCE，所以，∠G=∠A.又因为∠EDB=2∠A，所以，∠G=∠DEG，所以，DE=DG=6+8=14.从点E作EH垂直于BC，垂足为H，则
，
.根据勾股定理可知
.求得EC=16，所以BC=16.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，以等边三角形ABC的BC边为直径画半圆，分别交AB、AC于点E、D，DF是圆的切线，过点F作BC的垂线交BC于点G．若AF的长为2，则FG的长为
A. 4 B.
C. 6 D. 
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，直线
与
轴，
轴分别交于
，
两点．直线
与
交于点
且与轴，轴分别交于
，
．
图1 图2 图3
（1）求出点
坐标，直线
解析式；（2）如图2，点
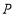为线段
上一点（不含端点），连接
，一动点
从出发，沿线段以每秒
个单位的速度运动到点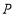，再沿线段
以每秒
个单位的速度运动到点
停止，求点在整个运动过程中所用最少时间时点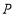的坐标；（3）如图3，平面直角坐标系中有一点
，使得
，求点
坐标． -
科目： 来源： 题型：
查看答案和解析>>【题目】一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮，球沿一条抛物线运动，当球运动的水平距离为2.5m时，达到最大高度3.5m，然后准确落入篮框内．已知篮圈中心距离地面高度为3.05m，在如图所示的平面直角坐标系中，下列说法正确的是（ ）
A. 此抛物线的解析式是y=﹣
x2+3.5B. 篮圈中心的坐标是（4，3.05）
C. 此抛物线的顶点坐标是（3.5，0）
D. 篮球出手时离地面的高度是2m
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，∠1=∠2，AE⊥OB于E，BD⊥OA于D，交点为C，则图中全等三角形共有（ ）
A. 2对 B. 3对 C. 4对 D. 5对
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA，过E作EF⊥AB，F为垂足．下列结论：①△ABD≌△EBC；②∠BCE+∠BCD=180°；③AD=AE=EC；④BA+BC=2BF；其中正确的是（ ）
A.①②③B.①③④C.①②④D.①②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校有1500名学生，为了解全校学生的上学方式，该校数学兴趣小组在全校随机抽取了100名学生进行抽样调查．整理样本数据，得到下列图表（频数分布表中部分划记被墨水盖住）：
某校100名学生上学方式频数分布表
方式
划记
频数
步行
正正正
15
骑车
正正正正正
29
乘公共交通工具
正正正正正正
30
乘私家车
其它
合计
100
（1）本次调查的个体是 ．
（2）求频数分布表中，“乘私家车”部分对应的频数．
（3）请估计该校1500名学生中，选择骑车、乘公交和步行上学的一共有多少人？
相关试题
