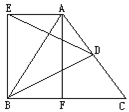
【题目】已知,如图,等边△ABC中,AD=DC,BF=FC,△BDE是等边三角形.求证:四边形AEBF是矩形.
参考答案:
【答案】见解析
【解析】
根据等边三角形的性质可得AF=BD=BE,再求出∠EBF=∠AFB=90°,连接EF,然后利用“边角边”证明△ABF和△EFB全等,根据全等三角形对应边相等可得AB=EF,再证出四边形AEBF是平行四边形,然后根据对角线相等的平行四边形是矩形证明即可.
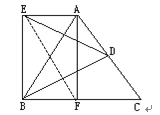
证明:连接EF,
∵等边△ABC中,点D是AC的中点,F是BC的中点,
∴AF=BD,∠CBD=30°,∠AFB=90°
∵△BDE是等边三角形,
∴BE=BD,∠DBE=60°,
∴∠EBF=∠DBE+∠CBD=90°
∴AF=BD=BE,∠EBF=∠AFB,
在△ABF和△EFB中,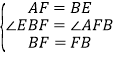
∴△ABF≌△EFB(SAS),
∴AB=EF,
∵∠AFB=∠EBF=90°,
∴AF∥BE,
又∵AF=BE,
∴四边形AEBF是平行四边形,
∵AB=EF,
∴四边形AEBF是矩形,
故AB=EF,且四边形AEBF是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】数学家华罗庚在一次出国访问途中,看到飞机上邻座的乘客阅读的杂志上有一道智力题:求59319的立方根.华罗庚脱口而出:39.众人感觉十分惊奇,请华罗庚给大家解读其中的奥秘.
你知道怎样迅速准确的计算出结果吗?请你按下面的问题试一试:
①
 ,又
,又 ,
, ,∴能确定59319的立方根是个两位数.
,∴能确定59319的立方根是个两位数.②∵59319的个位数是9,又
 ,∴能确定59319的立方根的个位数是9.
,∴能确定59319的立方根的个位数是9.③如果划去59319后面的三位319得到数59,
而
 ,则
,则 ,可得
,可得 ,
,由此能确定59319的立方根的十位数是3
因此59319的立方根是39.
(1)现在换一个数195112,按这种方法求立方根,请完成下列填空.
①它的立方根是_______位数.
②它的立方根的个位数是_______.
③它的立方根的十位数是__________.
④195112的立方根是________.
(2)请直接填写结果:
①
 ________.
________.②
 ________.
________. -
科目: 来源: 题型:
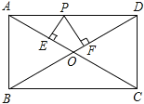
查看答案和解析>>【题目】如图,矩形ABCD的两边AB=3,BC=4,P是AD上任一点,PE⊥AC于点E,PF⊥BD于点F.求PE+PF的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B、D为线段AH上两点,△ABC、△BDE和△DGH都是等边三角形,连结CE并延长交AH的延长线于点F,点G恰好在CF上,△ABC的外接圆⊙O交CF于点M.
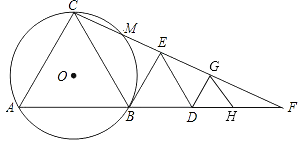
(1)求证:AC 2=CMCF;
(2)若CM=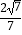 ,MF=
,MF= 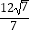 ,求圆O的半径长;
,求圆O的半径长;
(3)设等边△ABC、△BDE、△DGH的面积分别为S1、S2、S3 , 请直接写出S1、S2、S3之间的等量关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE平分∠BAD,交BC于点E,BF平分∠ABC,交AD于点F,AE与BF交于点P,连接EF,PD.
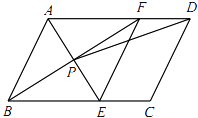
(1)求证:四边形ABEF是菱形;
(2)若AB=4,AD=6,∠ABC=60°,求tan∠ADP的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①平面内,垂直于同一直线的两条直线平行;②两条直线被第三条直线所截,内错角相等;③如果直线
 ,
, 那么
那么 ;④直线外一点与直线上各点连接的所有线段中,垂线段最短;⑤同旁内角的角平分线互相垂直.其中正确的是( )
;④直线外一点与直线上各点连接的所有线段中,垂线段最短;⑤同旁内角的角平分线互相垂直.其中正确的是( )A.①③④B.①②⑤C.②③④D.②③⑤
-
科目: 来源: 题型:
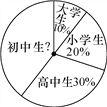
查看答案和解析>>【题目】某次学生夏令营活动,有小学生、初中生、高中生和大学生参加,共200人,各类学生人数比例见扇形统计图.
(1)参加这次夏令营活动的初中生共有多少人?
(2)活动组织者号召参加这次夏令营活动的所有学生为贫困学生捐款.结果小学生每人
捐款 5 元,初中生每人捐款 10 元,高中生每人捐款 15 元,大学生每人捐款 20 元.问平均 每人捐款是多少元?
(3)在(2)的条件下,把每个学生的捐款数额(以元为单位)——记录下来,则在这组数据中,众数是多少?
相关试题

