【题目】在平面直角坐标系中,点A(3,﹣2)在对称轴为直线x=2的抛物线y=x2+bx+c的图象上,其顶点为B.
(1)求顶点B的坐标;
(2)点C在对称轴上,若△ABC的面积为2,求点C的坐标;
(3)将抛物线向左或右平移,使得新抛物线的顶点落在y轴上,问原抛物线上是否存在点M,平移后的对应点为N,满足OM=ON?如果存在,求出点M,N的坐标;如果不存在,请说明理由.
参考答案:
【答案】(1)(2,-3);(2)(2,1)或(2,﹣7);(3)见解析.
【解析】分析:![]() 根据抛物线的对称轴为直线x=2,即可求出
根据抛物线的对称轴为直线x=2,即可求出![]() ,把点
,把点![]() 代入抛物线的解析式即可求出
代入抛物线的解析式即可求出![]() ,把抛物线的解析式通过配方变成顶点式,即可求出点
,把抛物线的解析式通过配方变成顶点式,即可求出点![]() 的坐标.
的坐标.
![]() 设
设![]() 则
则![]() 点A到对称轴的距离是1,
点A到对称轴的距离是1,![]() 求出
求出![]() 的值即可.
的值即可.
![]() 抛物线的顶点坐标为
抛物线的顶点坐标为![]() ,平移后抛物线的顶点坐标在y轴上,则抛物线向左平移了2个单位长度.平移后抛物线的解析式为:
,平移后抛物线的顶点坐标在y轴上,则抛物线向左平移了2个单位长度.平移后抛物线的解析式为:![]() MN=2.点M与点N关于y轴对称,设
MN=2.点M与点N关于y轴对称,设![]() 则
则![]() 分别代入解析式可得
分别代入解析式可得![]() 解得
解得![]()
即可求出点![]() 的坐标.
的坐标.
详解:(1)∵抛物线![]() 的对称轴为直线x=2,
的对称轴为直线x=2,
∴![]() ,
,
解得:![]()
∴![]()
把![]() 代入,得
代入,得![]()
解得![]()
∴该抛物线解析式为:![]()
顶点![]() 的坐标为:
的坐标为:![]()
(2)设![]() 则
则![]()
∵点A到对称轴的距离是1,
∴![]() 即a=1或
即a=1或![]()
∴点C的坐标是![]() 或
或![]() ;
;
(3)∵抛物线的顶点坐标为![]() ,平移后抛物线的顶点坐标在y轴上,
,平移后抛物线的顶点坐标在y轴上,
∴抛物线向左平移了2个单位长度.
∴平移后抛物线的解析式为:![]() MN=2.
MN=2.
∵![]()
∴点O在线段MN的垂直平分线上,
又MN∥x轴,
∴点M与点N关于y轴对称,
设![]() 则
则![]() 分别代入解析式可得
分别代入解析式可得![]()
解得![]()
∴点M的坐标为![]() 点N的坐标为
点N的坐标为![]() .即原抛物线存在点M,平移后的对应点为N,满足OM=ON,此时点M的坐标为
.即原抛物线存在点M,平移后的对应点为N,满足OM=ON,此时点M的坐标为![]() 点N的坐标为
点N的坐标为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,将一点(横坐标与纵坐标不相等)横坐标与纵坐标互换后得到的点叫这一点的“对称点”,如(2,﹣3)与(﹣3,2)是一对“对称点”.
(1)点(m,n)和它的“对称点“均在直线y=kx+a上,求k的值;
(2)直线y=kx+3与抛物线y=x2+bx+c的两个交点A,B恰好是“对称点”,其中点A在反比例函数y=
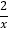 的图象上,求此抛物线的解析式.
的图象上,求此抛物线的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两块完全相同的直角三角形纸片的直角顶点
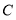 叠放在一起,若保持
叠放在一起,若保持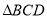 不动,将
不动,将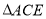 绕直角顶点
绕直角顶点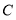 旋转.
旋转.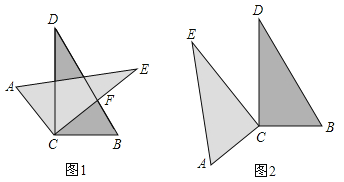
(1)当
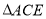 绕直角顶点
绕直角顶点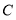 旋转到如图1的位置时,
旋转到如图1的位置时,①若
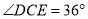 ,则
,则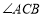 =_________°;若
=_________°;若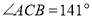 ,则
,则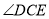 =_________°;
=_________°;②猜想
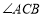 与
与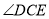 的数量关系为:_________;
的数量关系为:_________;(2)当
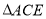 绕直角顶点
绕直角顶点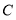 旋转到如图2的位置时,②中
旋转到如图2的位置时,②中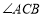 与
与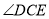 的数量关系是否仍然成立?请说明理由.(注:
的数量关系是否仍然成立?请说明理由.(注: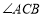 与
与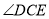 为小于平角的角)
为小于平角的角) -
科目: 来源: 题型:
查看答案和解析>>【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。

-
科目: 来源: 题型:
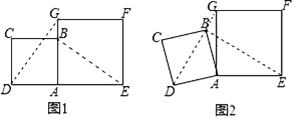
查看答案和解析>>【题目】在数学兴趣小组活动中,小明进行数学探究活动.将边长为2的正方形ABCD与边长为3的正方形AEFG按图1位置放置,AD与AE在同一条直线上,AB与AG在同一条直线上.
(1)小明发现DG=BE且DG⊥BE,请你给出证明.
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时△ADG的面积.
-
科目: 来源: 题型:
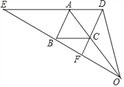
查看答案和解析>>【题目】如图,已知DE∥BC,AO,DF交于点C.∠EAB=∠BCF.
(1)求证:AB∥DF;
(2)求证:OB2=OEOF;
(3)连接OD,若∠OBC=∠ODC,求证:四边形ABCD为菱形.
-
科目: 来源: 题型:
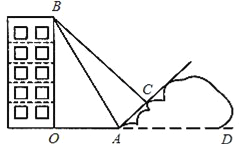
查看答案和解析>>【题目】某校九年级的小红同学,在自己家附近进行测量一座楼房高度的实践活动.如图,她在山坡坡脚A出测得这座楼房的楼顶B点的仰角为60°,沿山坡往上走到C处再测得B点的仰角为45°.已知OA=200m,此山坡的坡比i=
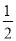 ,且O、A、D在同一条直线上.
,且O、A、D在同一条直线上.求:(1)楼房OB的高度;
(2)小红在山坡上走过的距离AC.(计算过程和结果均不取近似值)
相关试题

