【题目】在平面直角坐标系中,将一点(横坐标与纵坐标不相等)横坐标与纵坐标互换后得到的点叫这一点的“对称点”,如(2,﹣3)与(﹣3,2)是一对“对称点”.
(1)点(m,n)和它的“对称点“均在直线y=kx+a上,求k的值;
(2)直线y=kx+3与抛物线y=x2+bx+c的两个交点A,B恰好是“对称点”,其中点A在反比例函数y=![]() 的图象上,求此抛物线的解析式.
的图象上,求此抛物线的解析式.
参考答案:
【答案】(1)﹣1;(2)y=x2﹣4x+5.
【解析】分析:![]() 把点
把点![]() 和它的对称点
和它的对称点![]() 代入一次函数解析式,即可求出k的值;
代入一次函数解析式,即可求出k的值;
![]() 设点A的坐标为
设点A的坐标为![]() ,点A在反比例函数
,点A在反比例函数![]() 的图象上,则
的图象上,则![]() ,
,
由(1)知![]() 求出
求出![]() 的值,继而写成点
的值,继而写成点![]() 的坐标,用待定系数法即可求得抛物线的解析式.
的坐标,用待定系数法即可求得抛物线的解析式.
详解:(1)由题意可得,点![]() 和点
和点![]() 都在直线
都在直线![]() 上,
上,
![]() 解得:
解得:![]()
即k的值是![]() ;
;
(2)设点A的坐标为![]() ,点A在反比例函数
,点A在反比例函数![]() 的图象上,则
的图象上,则![]() ,
,
由(1)知![]()
∴![]() 得
得![]() 或
或![]() ,
,
∴这一对对称点是![]() 和
和![]()
∵抛物线![]() 的两个交点A,B恰好是“对称点”,
的两个交点A,B恰好是“对称点”,
∴![]() 解得:
解得:![]()
∴此抛物线的解析式为:![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数y =(2m+1) x+ m-3
(1) 若函数图象经过原点,求m的值.
(2) 若函数图象在y轴的交点的纵坐标为-2,求m的值.
(3)若函数的图象平行直线y=-3x–3,求m的值.
(4)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校办公楼前有一长为
 ,宽为
,宽为 的长方形空地,在中心位置留出一个半径为
的长方形空地,在中心位置留出一个半径为 的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
的圆形区域建一个喷泉,两边是两块长方形的休息区,阴影部分为绿地.
(1)用含字母和
 的式子表示阴影部分的面积;
的式子表示阴影部分的面积;(2)当
 =4,
=4, =3,
=3, =1,
=1, =2时,阴影部分面积是多少?(
=2时,阴影部分面积是多少?( 取3)
取3) -
科目: 来源: 题型:
查看答案和解析>>【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数.(如下表)
每人加工零件数
54
45
30
24
21
12
人 数
1
1
2
6
3
2
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理?为什么?如果不合理,请你设计一个较为合理的生产定额,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将两块完全相同的直角三角形纸片的直角顶点
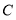 叠放在一起,若保持
叠放在一起,若保持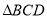 不动,将
不动,将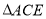 绕直角顶点
绕直角顶点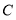 旋转.
旋转.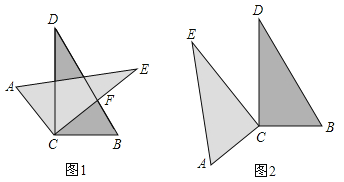
(1)当
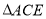 绕直角顶点
绕直角顶点 旋转到如图1的位置时,
旋转到如图1的位置时,①若
 ,则
,则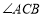 =_________°;若
=_________°;若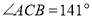 ,则
,则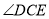 =_________°;
=_________°;②猜想
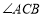 与
与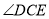 的数量关系为:_________;
的数量关系为:_________;(2)当
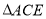 绕直角顶点
绕直角顶点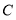 旋转到如图2的位置时,②中
旋转到如图2的位置时,②中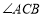 与
与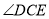 的数量关系是否仍然成立?请说明理由.(注:
的数量关系是否仍然成立?请说明理由.(注: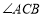 与
与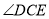 为小于平角的角)
为小于平角的角) -
科目: 来源: 题型:
查看答案和解析>>【题目】(11·湖州)(本小题10分)
如图,已知E、F分别是□ABCD的边BC、AD上的点,且BE=DF。
⑴求证:四边形AECF是平行四边形;
⑵若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长。

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A(3,﹣2)在对称轴为直线x=2的抛物线y=x2+bx+c的图象上,其顶点为B.
(1)求顶点B的坐标;
(2)点C在对称轴上,若△ABC的面积为2,求点C的坐标;
(3)将抛物线向左或右平移,使得新抛物线的顶点落在y轴上,问原抛物线上是否存在点M,平移后的对应点为N,满足OM=ON?如果存在,求出点M,N的坐标;如果不存在,请说明理由.
相关试题

