【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F. 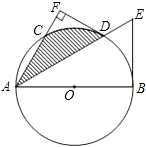
(1)求证:DF是⊙O的切线;
(2)若DF=3,DE=2 ①求 ![]() 值;
值;
②求图中阴影部分的面积.
参考答案:
【答案】
(1)证明:连接OD
∵OA=OD,∴∠1=∠2
∵∠1=∠3,∴∠2=∠3
∴OD∥AF
∵DF⊥AF,∴OD⊥DF
∴DF是⊙O的切线
(2)证明:①解:连接BD
∵直径AB
∴∠ADB=90°
∵圆O与BE相切
∴∠ABE=90°
∵∠DAB+∠DBA=∠DBA+∠DBE=90°
∴∠DAB=∠DBE
∴∠DAB=∠FAD
∵∠AFD=∠BDE=90°
∴△BDE∽△AFD
∴ ![]()
②连接OC,交AD于G
由①,设BE=2x,则AD=3x
∵△BDE∽△ABE∴ ![]()
∴ ![]()
解得:x1=2, ![]() (不合题意,舍去)
(不合题意,舍去)
∴AD=3x=6,BE=2x=4,AE=AD+DE=8
∴AB= ![]() ,∠1=30°
,∠1=30°
∴∠2=∠3=∠1=30°,∴∠COD=2∠3=60°
∴∠OGD=90°=∠AGC,∴AG=DG
∴△ACG≌△DOG,∴S△AGC=S△DGO
∴S阴影=S扇形COD= ![]()
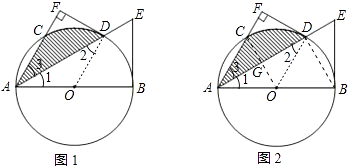
【解析】(1)作辅助线,连接OD.根据切线的判定定理,只需证DF⊥OD即可;(2)①连接BD.根据BE、DF两切线的性质证明△BDE∽△ABE;又由角平分线的性质、等腰三角形的两个底角相等求得△ABE∽△AFD,所以△BDE∽△AFD;最后由相似三角形的对应边成比例求得 ![]() ;②连接OC,交AD于G.由①,设BE=2x,则AD=3x.利用①中的△BDE∽△ABE的对应边成比例的性质求得
;②连接OC,交AD于G.由①,设BE=2x,则AD=3x.利用①中的△BDE∽△ABE的对应边成比例的性质求得 ![]() ,据此列出关于x的方程,解方程求得x=2,继而可以求出AD=3x=6,BE=2x=4,AE=AD+DE=8;然后由勾股定理知AB=4
,据此列出关于x的方程,解方程求得x=2,继而可以求出AD=3x=6,BE=2x=4,AE=AD+DE=8;然后由勾股定理知AB=4 ![]() ,在直角三角形ABE中求得∠1=30°;再由三角形的角平分线的性质、等腰三角形的性质及边角关系求得AG=DG,所以△ACG≌△DOG;最后根据两个全等三角形的面积相等的性质求扇形的面积即可.
,在直角三角形ABE中求得∠1=30°;再由三角形的角平分线的性质、等腰三角形的性质及边角关系求得AG=DG,所以△ACG≌△DOG;最后根据两个全等三角形的面积相等的性质求扇形的面积即可.
【考点精析】本题主要考查了勾股定理的概念和扇形面积计算公式的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请观察下列算式,找出规律并填空。
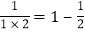 ,
,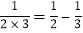 ,
,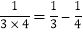 ,
,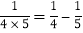 ···
···根据以上规律解答以下三题:
(1) 第10个等式是:__________=_____________
第n个等式是:__________=_____________
(2)计算:
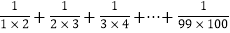 的值。
的值。(3)若有理数
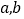 满足
满足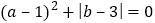 ,试求:
,试求: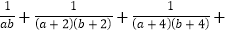
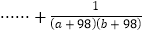 的值。
的值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】“红树林小组”全体组员参加了义务植树活动,领得准备种植的树苗一批,组长决定采用分工负责制,经计算发现:若每位组员种植10棵树苗,则还剩88棵;若每位组员种植12棵树苗,则有一位组员种植的树苗不到4棵,求准备种植树苗的棵数和“红树林小组”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在密码学中,直接可以看到的内容为明码,对明码进行某种处理后得到的内容为密码,有一种密码,将英文26个字母a,b,c,…,z(不论大写)依次对应1,2,3,…,26,这26个自然数,当明码字母对应的序号x为奇数时,密码字母对应的序号是
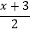 ;当明码字母对应的序号x为偶数时,密码存对应的序号是
;当明码字母对应的序号x为偶数时,密码存对应的序号是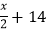 .按上述规定,将明码"hope”译成密码是( )
.按上述规定,将明码"hope”译成密码是( )
A. gawp B. rivd C. gihe D. hope
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2﹣2ax﹣b(a>0)与x轴的一个交点为B(﹣1,0),与y轴的负半轴交于点C,顶点为D.
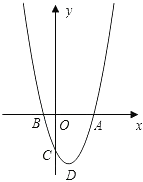
(1)直接写出抛物线的对称轴,及抛物线与x轴的另一个交点A的坐标;
(2)以AD为直径的圆经过点C.
①求抛物线的解析式;
②点E在抛物线的对称轴上,点F在抛物线上,且以B,A,F,E四点为顶点的四边形为平行四边形,求点F的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
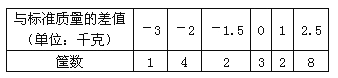
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价26元,则出售这20筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P1(x1 , y1),P2(x2 , y2)在反比例函数y=
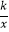 (k>0)的图像上,且x1=﹣x2 , 则( )
(k>0)的图像上,且x1=﹣x2 , 则( )
A.y1<y2
B.y1=y2
C.y1>y2
D.y1=﹣y2
相关试题

