【题目】如图,已知抛物线y=ax2﹣2ax﹣b(a>0)与x轴的一个交点为B(﹣1,0),与y轴的负半轴交于点C,顶点为D.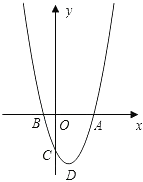
(1)直接写出抛物线的对称轴,及抛物线与x轴的另一个交点A的坐标;
(2)以AD为直径的圆经过点C.
①求抛物线的解析式;
②点E在抛物线的对称轴上,点F在抛物线上,且以B,A,F,E四点为顶点的四边形为平行四边形,求点F的坐标.
参考答案:
【答案】
(1)
解:对称轴是直线:x=1,
点A的坐标是(3,0)
(2)
解:①如图,连接AC、AD,过D作DM⊥y轴于点M,

解法一:利用△AOC∽△CMD,
在y=ax2﹣2ax﹣b(a>0)中,当x=1时,y=﹣a﹣b,则D的坐标是(1,﹣a﹣b).
∵点A、D、C的坐标分别是A(3,0),D(1,﹣a﹣b)、
C(0,﹣b),
∴AO=3,MD=1.
由 ![]() ,
,
得 ![]() ,
,
∴3﹣ab=0.
又∵0=a(﹣1)2﹣2a(﹣1)﹣b,
∴由 ![]() ,
,
得 ![]() ,
,
∴函数解析式为:y=x2﹣2x﹣3.
解法二:利用以AD为直径的圆经过点C,
∵点A、D的坐标分别是A(3,0)、D(1,﹣a﹣b)、C(0,﹣b),
∴AC= ![]() ,CD=
,CD= ![]() ,AD=
,AD= ![]()
∵AC2+CD2=AD2
∴3﹣ab=0①
又∵0=a(﹣1)2﹣2a(﹣1)﹣b②
由①、②得a=1,b=3
∴函数解析式为:y=x2﹣2x﹣3.
②F点存在.
如图所示,当四边形BAFE为平行四边形时
则BA∥EF,并且BA=EF.
∵BA=4,
∴EF=4
由于对称轴为x=1,
∴点F的横坐标为5.
将x=5代入y=x2﹣2x﹣3得y=12,∴F(5,12).
根据抛物线的对称性可知,在对称轴的左侧抛物线上也存在点F,
使得四边形BAEF是平行四边形,此时点F坐标为(﹣3,12).
当四边形BEAF是平行四边形时,点F即为点D,
此时点F的坐标为(1,﹣4).
综上所述,点F的坐标为(5,12),(﹣3,12)或(1,﹣4).

【解析】(1)已知抛物线解析式和点B的坐标求出a值,利用对称轴x=﹣ ![]() 求出对称轴以及点A的坐标.(2)①本题要靠辅助线的帮助.连接AC,AD,过DM⊥y轴于点M.证明△AOC∽△CMD后可推出a,b的值.②证明四边形BAFE为平行四边形,求出BA,EF得出点F的坐标.
求出对称轴以及点A的坐标.(2)①本题要靠辅助线的帮助.连接AC,AD,过DM⊥y轴于点M.证明△AOC∽△CMD后可推出a,b的值.②证明四边形BAFE为平行四边形,求出BA,EF得出点F的坐标.
【考点精析】利用二次函数的图象和二次函数的性质对题目进行判断即可得到答案,需要熟知二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“红树林小组”全体组员参加了义务植树活动,领得准备种植的树苗一批,组长决定采用分工负责制,经计算发现:若每位组员种植10棵树苗,则还剩88棵;若每位组员种植12棵树苗,则有一位组员种植的树苗不到4棵,求准备种植树苗的棵数和“红树林小组”的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在密码学中,直接可以看到的内容为明码,对明码进行某种处理后得到的内容为密码,有一种密码,将英文26个字母a,b,c,…,z(不论大写)依次对应1,2,3,…,26,这26个自然数,当明码字母对应的序号x为奇数时,密码字母对应的序号是
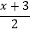 ;当明码字母对应的序号x为偶数时,密码存对应的序号是
;当明码字母对应的序号x为偶数时,密码存对应的序号是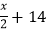 .按上述规定,将明码"hope”译成密码是( )
.按上述规定,将明码"hope”译成密码是( )
A. gawp B. rivd C. gihe D. hope
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
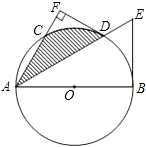
(1)求证:DF是⊙O的切线;
(2)若DF=3,DE=2 ①求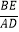 值;
值;
②求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
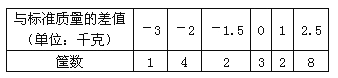
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价26元,则出售这20筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点P1(x1 , y1),P2(x2 , y2)在反比例函数y=
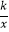 (k>0)的图像上,且x1=﹣x2 , 则( )
(k>0)的图像上,且x1=﹣x2 , 则( )
A.y1<y2
B.y1=y2
C.y1>y2
D.y1=﹣y2 -
科目: 来源: 题型:
查看答案和解析>>【题目】大家知道,
 它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子
它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子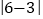 ,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=
,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=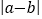 .根据
.根据以上信息,回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ;数轴上表示-2和-5的两点之间的距离是 .
(2)点A、B在数轴上分别表示实数x和
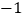 .
.①用代数式表示A、B两点之间的距;
②如果
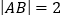 ,求x的值.
,求x的值.(3)直接写出代数式
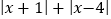 的最小值.
的最小值.
相关试题

