【题目】若点P1(x1 , y1),P2(x2 , y2)在反比例函数y= ![]() (k>0)的图像上,且x1=﹣x2 , 则( )
(k>0)的图像上,且x1=﹣x2 , 则( )
A.y1<y2
B.y1=y2
C.y1>y2
D.y1=﹣y2
参考答案:
【答案】D
【解析】解:∵点P1(x1 , y1),P2(x2 , y2)在反比例函数y= ![]() (k>0)的图像上,
(k>0)的图像上,
∴y1= ![]() ,y2=
,y2= ![]() ,
,
∵x1=﹣x2 ,
∴y1= ![]() =﹣
=﹣ ![]()
∴y1=﹣y2 .
故选D.
【考点精析】通过灵活运用反比例函数的图象和反比例函数的性质,掌握反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点;性质:当k>0时双曲线的两支分别位于第一、第三象限,在每个象限内y值随x值的增大而减小; 当k<0时双曲线的两支分别位于第二、第四象限,在每个象限内y值随x值的增大而增大即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是⊙O的直径,C是⊙O上一点,∠BAC的平分线交⊙O于点D,交⊙O的切线BE于点E,过点D作DF⊥AC,交AC的延长线于点F.
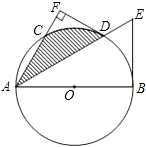
(1)求证:DF是⊙O的切线;
(2)若DF=3,DE=2 ①求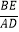 值;
值;
②求图中阴影部分的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2﹣2ax﹣b(a>0)与x轴的一个交点为B(﹣1,0),与y轴的负半轴交于点C,顶点为D.
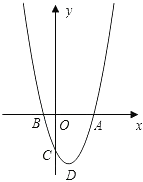
(1)直接写出抛物线的对称轴,及抛物线与x轴的另一个交点A的坐标;
(2)以AD为直径的圆经过点C.
①求抛物线的解析式;
②点E在抛物线的对称轴上,点F在抛物线上,且以B,A,F,E四点为顶点的四边形为平行四边形,求点F的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
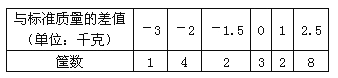
(1)20筐白菜中,最重的一筐比最轻的一筐重多少千克?
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价26元,则出售这20筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】大家知道,
 它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子
它在数轴上表示5的点与原点(即表示0的点)之间的距离.又如式子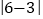 ,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=
,它在数轴上的意义是表示6的点与表示3的点之间的距离.即点A、B在数轴上分别表示数a、b,则A、B两点的距离可表示为:|AB|=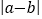 .根据
.根据以上信息,回答下列问题:
(1)数轴上表示2和5的两点之间的距离是 ;数轴上表示-2和-5的两点之间的距离是 .
(2)点A、B在数轴上分别表示实数x和
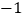 .
.①用代数式表示A、B两点之间的距;
②如果
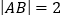 ,求x的值.
,求x的值.(3)直接写出代数式
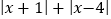 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,AD⊥BC交直线BC于点D,若AD=
 BC,则△ABC的顶角的度数为:________
BC,则△ABC的顶角的度数为:________ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,BC=15,斜边AB的垂直平分线与∠CAB的平分线都交BC于D点,则点D到斜边AB的距离为________.

相关试题

