【题目】如图,已知∠AOB内部有三条射线,OE平分∠BOC,OF平分∠AOC.
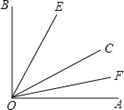
(1)若∠AOB=90°,∠AOC=30°,求∠EOF的度数;
(2)若∠AOB=![]() ,求∠EOF的度数(写出求解过程);
,求∠EOF的度数(写出求解过程);
(3)若将条件中“OE平分∠BOC,OF平分∠AOC.平分”改为“∠EOB=![]() ∠COB,∠COF=
∠COB,∠COF=![]() ∠COA”,且∠AOB=
∠COA”,且∠AOB=![]() ,求∠EOF的度数(写出求解过程).
,求∠EOF的度数(写出求解过程).
参考答案:
【答案】(1)∠EOF=45°;(2)∠EOF=![]() ;(3)∠EOF=
;(3)∠EOF=![]() .
.
【解析】
根据角平分线的定义,利用角的和差即可得出答案.
∵∠AOB=90°,∠AOC=30°,
∴∠COB=60°;
∵OE平分∠BOC,OF平分∠AOC,
∴∠FOC=15°,∠EOC=30°,
∴∠EOF=∠EOC+∠FOC=45°
∵∠AOB=![]() ,OE平分∠BOC,OF平分∠AOC,
,OE平分∠BOC,OF平分∠AOC,
∴∠EOF=∠EOC+∠FOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=
∠AOB=![]()
![]() ;
;
∵∠AOB=![]() ,∠EOB=
,∠EOB=![]() ∠COB,∠COF=
∠COB,∠COF=![]() ∠COA,
∠COA,
∴∠EOF=∠EOC+∠FOC=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=
∠AOB=![]()
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时
 张用A方法,其余用B方法。
张用A方法,其余用B方法。(1)用
 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
-
科目: 来源: 题型:
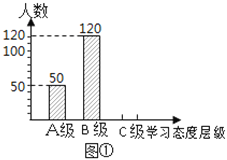
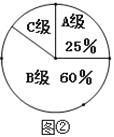
查看答案和解析>>【题目】某市教育局对该市部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了________名学生;
(2)图②中C级所占的圆心角的度数是__________;
(3)根据抽样调查结果,请你估计该市近20000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电脑公司经销甲种型号电脑,每台售价4000元.为了增加收入,电脑公司决定再经销乙种型号电脑.已知甲种电脑每台进价为3500元,乙种电脑每台进价为3000元,公司预计用不多于5万元且不少于4.8万元的资金购进这两种电脑共15台.
(1)有几种进货方案?
(2)如果乙种电脑每台售价为3800元,为打开乙种电脑的销路,公司决定每售出一台乙种电脑,返还顾客现金a元,要使(2)中所有方案获利相同,a值应是多少? 若考虑投入成本最低,则应选择哪种进货方案?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O是△ABC的外心,I是△ABC的内心,连AI并延长交BC和⊙O于D、E两点.
(1)求证:EB=EI;
(2)若AB=4,AC=3,BE=2,求AI的长.

-
科目: 来源: 题型:
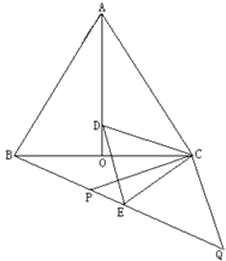
查看答案和解析>>【题目】如图,等边△ABC中,AO是∠BAC的角平分线,D为AO上一点,以CD为一边且在CD下方作等边△CDE,连接BE.
(1)求证:△ACD≌△BCE;
(2)延长BE至Q,P为BQ上一点,连接CP、CQ使CP=CQ=5,若BC=8时,求PQ的长.
-
科目: 来源: 题型:
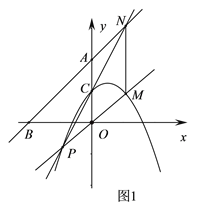
查看答案和解析>>【题目】已知,抛物线y=-
 x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.
x2 +bx+c交y轴于点C(0,2),经过点Q(2,2).直线y=x+4分别交x轴、y轴于点B、A.(1)直接填写抛物线的解析式________;
(2)如图1,点P为抛物线上一动点(不与点C重合),PO交抛物线于M,PC交AB于N,连MN.
求证:MN∥y轴;
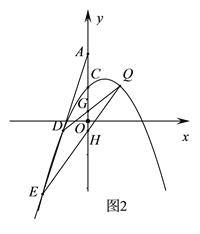
(3)如图,2,过点A的直线交抛物线于D、E,QD、QE分别交y轴于G、H.求证:CG CH为定值.
相关试题