【题目】如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4 , 给出如下结论: ①S1+S2=S3+S4;②S2+S4=S1+S3;③若S3=2S1 , 则S4=2S2;④若S1=S2 , 则P点在矩形的对角线上.
其中正确的结论的序号是(把所有正确结论的序号都填在横线上).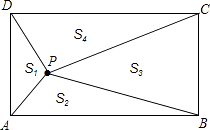
参考答案:
【答案】②和④
【解析】解:如右图,过点P分别作PF⊥AD于点F,PE⊥AB于点E, ∵△APD以AD为底边,△PBC以BC为底边,
∴此时两三角形的高的和为AB,即可得出S1+S3= ![]() 矩形ABCD面积;
矩形ABCD面积;
同理可得出S2+S4= ![]() 矩形ABCD面积;
矩形ABCD面积;
∴S2+S4=S1+S3(故②正确);
当点P在矩形的两条对角线的交点时,S1+S2=S3+S4 . 但P是矩形ABCD内的任意一点,所以该等式不一定成立.(故①不一定正确);
③若S3=2S1 , 只能得出△APD与△PBC高度之比,S4不一定等于2S2;(故③错误);
④若S1=S2 , ![]() ×PF×AD=
×PF×AD= ![]() PE×AB,
PE×AB,
∴△APD与△PBA高度之比为: ![]() =
= ![]() ,
,
∵∠DAE=∠PEA=∠PFA=90°,
∴四边形AEPF是矩形,
∴此时矩形AEPF与矩形ABCD相似,
∴ ![]() =
= ![]() ,
,
∴P点在矩形的对角线上.(故④选项正确)
故答案为:②和④.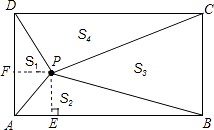
根据三角形面积求法以及矩形性质得出S1+S3= ![]() 矩形ABCD面积,以及
矩形ABCD面积,以及 ![]() =
= ![]() ,
, ![]() =
= ![]() ,即可得出P点一定在AC上.
,即可得出P点一定在AC上.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:x2﹣6x+8=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2x+5y﹣3=0,求4x32y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列
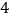 个命题:其中真命题是( ).
个命题:其中真命题是( ).
⑴三角形的外角和是 ;⑵三角形的三个内角中至少有两个锐角;⑶直角三角形两锐角互余;⑷相等的角是对顶角.
;⑵三角形的三个内角中至少有两个锐角;⑶直角三角形两锐角互余;⑷相等的角是对顶角.
A.( )(
)( 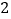 )
)
B.(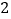 )(
)( 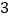 )
)
C.(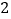 )(
)( 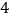 )
)
D.( )(
)(  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
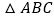 中,
中, 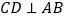 ,垂足为
,垂足为 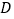 ,点
,点 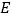 在
在 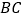 上,
上, 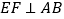 ,垂足为
,垂足为 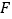 .
.
(1)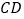 与
与 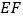 平行吗?为什么?
平行吗?为什么?
(2)如果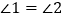 ,且
,且 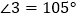 ,求
,求 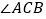 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,AD=4,E为AD边上一动点(不与点A重合),AF⊥BE,垂足为F,GF⊥CF,交AB于点G,连接EG.设AE=x,S△BEG=y.
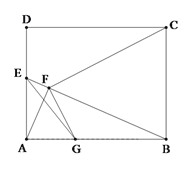
(1)证明:△AFG∽△BFC;
(2)求y与x的函数关系式,并求出y的最大值;
(3)若△BFC为等腰三角形,请直接写出x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数的图象y1=kx+b与反比例函数
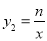 的图象交于点A(1,5)和点B(m,1).
的图象交于点A(1,5)和点B(m,1).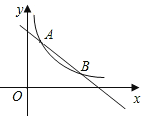
(1)求m的值和反比例函数的解析式;
(2)当x>0时,根据图象直接写出不等式
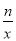 ≥kx+b的解集;
≥kx+b的解集;(3)若经过点B的抛物线的顶点为A,求该抛物线的解析式.
相关试题

