【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC,外角∠CAM的平分线,CE⊥AN,垂足为点E.
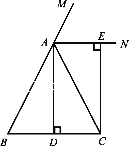
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
参考答案:
【答案】(1)证明见解析;
(2)当AD= ![]() 时,四边形ADCE是正方形,证明见解析.
时,四边形ADCE是正方形,证明见解析.
【解析】试题分析:(1)求出∠BAD=∠DAC,∠MAE=∠CAE,求出∠DAE的度数,求出∠AEC=∠ADC=∠EAD=90°,根据矩形的判定判断即可;
(2)求出AD=DC,得出∠ACD=∠DAC=45°,求出∠BAC=90°,即可求出答案.
试题解析:(1)证明:∵在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE.
∴∠DAE=∠DAC+∠CAE=![]() ∠MAC+
∠MAC+![]() ∠CAB=
∠CAB=![]() ×180°=90°,
×180°=90°,
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
(2)证明:∵四边形ADCE是正方形,
∴DC=AD,
∵在△ABC中,AB=AC,AD⊥BC,
∴△ADC为等腰直角三角形,
∴∠DAC=∠ACD=45°,
∴∠BAC=90°,
∴△ABC为等腰直角三角形,
即△ABC的形状是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.根据两人的作法可判断( )
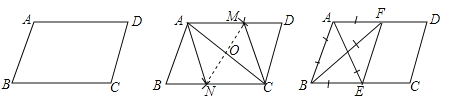
A. 甲正确,乙错误 B. 乙正确,甲错误
C. 甲、乙均正确 D. 甲、乙均错误
-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市美化工程招标时,有甲、乙两个工程队投标.经测算:甲队单独完成这项工程需要60天;若由甲队先做20天,剩下的工程由甲、乙合做24天可完成.
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲乙两队全程合作完成该工程省钱?
-
科目: 来源: 题型:
查看答案和解析>>【题目】
 是等边三角形,点
是等边三角形,点 是射线
是射线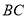 上的一个动点(点
上的一个动点(点 不与点
不与点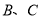 重合),
重合),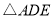 是以
是以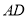 为边的等边三角形,过点
为边的等边三角形,过点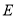 作
作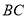 的平行线,分别交射线
的平行线,分别交射线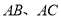 于点
于点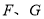 ,连接
,连接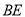 .
.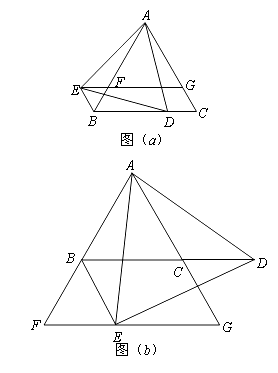
(1)如图(a)所示,当点
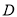 在线段
在线段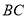 上时,
上时,①求证:
 ;
;②探究:四边形
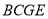 是怎样特殊的四边形?并说明理由;
是怎样特殊的四边形?并说明理由;(2)如图(b)所示,当点
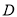 在
在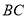 的延长线上时,
的延长线上时,①第(1)题中所求证和探究的两个结论是否仍然成立?(直接写出,不必说明理由)
②当点
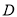 运动到什么位置时,四边形
运动到什么位置时,四边形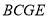 是菱形?并说明理由.
是菱形?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某多边形内角和与外角和共 1080°,则这个多边形的边数为( )
A.6B.7C.8D.9
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD中,CD=6cm,当边CD向右平移时,长方形的面积发生了变化.
(1)这个变化过程中,自变量、因变量各是什么?
(2)如果BC的长为
 cm,那么长方形的面积
cm,那么长方形的面积 可以表为 .
可以表为 .(3)当BC的长从12cm增加到20cm时,长方形的面积增加了多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC 的三个内角之比为 1:5:3,那么△ABC 中最大角的度数为_____.
相关试题

