【题目】如图,在平面直角坐标系xOy中,直线y=2x+2与y轴交于点A,与x轴交于点B.直线l⊥x轴负半轴于点C,点D是直线l上一点且位于x轴上方.已知CO=CD=4.
(1)求经过A,D两点的直线的函数关系式和点B的坐标;

(2)在直线l上是否存在点P使得△BDP为等腰三角形,若存在,直接写出P点坐标,若不存在,请说明理由.
参考答案:
【答案】(1)点B的坐标为(-1,0)直线AD的函数表达式为y=-![]() x+2;(2)存在,P1(-4,9),P2(-4,-4),P3(-4,-1),P4(-4,
x+2;(2)存在,P1(-4,9),P2(-4,-4),P3(-4,-1),P4(-4, ![]() ).
).
【解析】(1)用待定系数法即可求出直线的解析式;
(2)根据等腰三角形的两边相等,分BD、DP、BP分别为底即可得出答案.
解:(1)对于直线y=2x+2,当x=0时,y=2;当y=0时,x=-1

∴点A的坐标为(0,2),点B的坐标为(-1,0)
又∵CO=CD=4,
∴点D的坐标为(-4,4)
设直线AD的函数表达式为y=kx+b,则有![]() ,解得
,解得 ,
,
∴直线AD的函数表达式为y=-![]() x+2;
x+2;
(2)存在.共有四个点满足要求.
分别是P1(-4,9),P2(-4,-4),P3(-4,-1),P4(-4, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某批发门市销售两种商品,甲种商品每件售价为300元,乙种商品每件售价为80元.新年来临之际,该门市为促销制定了两种优惠方案:
方案一:买一件甲种商品就赠送一件乙种商品;
方案二:按购买金额打八折付款.
某公司为奖励员工,购买了甲种商品20件,乙种商品x(x≥20)件.
(1)分别写出优惠方案一购买费用y1(元)、优惠方案二购买费用y2(元)与所买乙种商品x(件)之间的函数关系式;
(2)若该公司共需要甲种商品20件,乙种商品40件.设按照方案一的优惠办法购买了m件甲种商品,其余按方案二的优惠办法购买.请你写出总费用w与m之间的关系式;利用w与m之间的关系式说明怎样购买最实惠.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平行四边形ABCD中,点E在直线AD上,AE=
 AD,连接CE交BD于点F,则EF:FC的值是 .
AD,连接CE交BD于点F,则EF:FC的值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.
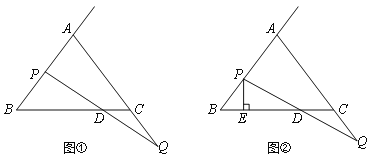
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC>∠ADC,且∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E,则∠AEC与∠ADC、∠ABC 之间存在的等量关系是( )

A. ∠AEC=∠ABC﹣2∠ADC B. ∠AEC=

C. ∠AEC=
 ∠ABC﹣∠ADC D. ∠AEC=
∠ABC﹣∠ADC D. ∠AEC= 
相关试题

