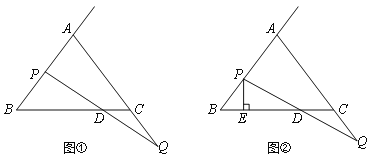
【题目】已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.
参考答案:
【答案】(1)CD=![]() ;(2)线段DE的长度保持不变,理由见解析.
;(2)线段DE的长度保持不变,理由见解析.
【解析】(1)过P点作PF∥AC交BC于F,即可构成小等边三角形BPF,再证明△PFD≌△QCD即可求解;
(2)根据(1)分两种情况:点P在线段AB上时,点P在BA的延长线上时分别求解即可得出结论.
解:(1)过P点作PF∥AC交BC于F,
∵点P为AB的中点,∴BP=![]() A B=3,
A B=3,
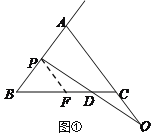
∵AB=AC=BC ,∴∠B=∠ACB=∠BAC=60°,
∵PF∥AC,∴∠PFB=∠ACB=60°,∠BPF=∠BAC=60°,
∴△PBF是等边三角形,
∴BF=FP=BP=3,∴FC=BC-BF=3,
由题意,BP=CQ,∴FP=CQ,
∵PF∥AC,∴∠DPF=∠DQC,
又∠PDF=∠QDC,∴△PFD≌△QCD,
∴CD=DF=![]() FC=
FC= ![]() ;
;
(2)当点P,Q在移动的过程中,线段DE的长度保持不变,
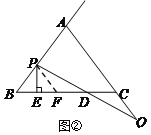
分两种情况讨论:
①当点P在线段AB上时,
过点P作PF∥AC交BC于F,由(1)知PB=PF,
∵PE⊥BC,∴BE=EF,
由(1)知△PFD≌△QCD,CD=DF,
∴DE=EF+DF=![]() BC=3,
BC=3,
②当点P在BA的延长线上时,同理可得DE=3,
∴当点P、Q在移动的过程中,线段DE的长度保持不变.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN是⊙O的直径,MN=4,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,则PA+PB的最小值为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平行四边形ABCD中,点E在直线AD上,AE=
 AD,连接CE交BD于点F,则EF:FC的值是 .
AD,连接CE交BD于点F,则EF:FC的值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=2x+2与y轴交于点A,与x轴交于点B.直线l⊥x轴负半轴于点C,点D是直线l上一点且位于x轴上方.已知CO=CD=4.
(1)求经过A,D两点的直线的函数关系式和点B的坐标;

(2)在直线l上是否存在点P使得△BDP为等腰三角形,若存在,直接写出P点坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC>∠ADC,且∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E,则∠AEC与∠ADC、∠ABC 之间存在的等量关系是( )

A. ∠AEC=∠ABC﹣2∠ADC B. ∠AEC=

C. ∠AEC=
 ∠ABC﹣∠ADC D. ∠AEC=
∠ABC﹣∠ADC D. ∠AEC= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C,其中正确的结论有___________.

相关试题

