【题目】如图,等边三角形的顶点A(1,1)、B(3,1),规定把等边△ABC“先沿x轴翻折,再向左平移1个单位”为一次変换,如果这样连续经过2016次变换后,等边△ABC的顶点C的坐标为 . 
参考答案:
【答案】(2018, ![]() +1)
+1)
【解析】解:∵△ABC是等边三角形AB=3﹣1=2,
∴点C到x轴的距离为1+2× ![]() =
= ![]() +1,
+1,
横坐标为2,
∴A(2, ![]() +1),
+1),
第2016次变换后的三角形在x轴上方,
点A的纵坐标为 ![]() +1,
+1,
横坐标为2+2016×1=2018,
所以,点A的对应点A′的坐标是(2018, ![]() +1),
+1),
所以答案是:(2018, ![]() +1).
+1).
【考点精析】认真审题,首先需要了解等边三角形的性质(等边三角形的三个角都相等并且每个角都是60°),还要掌握翻折变换(折叠问题)(折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在平行四边形ABCD中,点E在直线AD上,AE=
 AD,连接CE交BD于点F,则EF:FC的值是 .
AD,连接CE交BD于点F,则EF:FC的值是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=2x+2与y轴交于点A,与x轴交于点B.直线l⊥x轴负半轴于点C,点D是直线l上一点且位于x轴上方.已知CO=CD=4.
(1)求经过A,D两点的直线的函数关系式和点B的坐标;

(2)在直线l上是否存在点P使得△BDP为等腰三角形,若存在,直接写出P点坐标,若不存在,请说明理由.
-
科目: 来源: 题型:
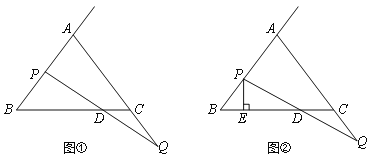
查看答案和解析>>【题目】已知△ABC中,AB=AC=BC=6.点P射线BA上一点,点Q是AC的延长线上一点,且BP=CQ,连接PQ,与直线BC相交于点D.
(1)如图①,当点P为AB的中点时,求CD的长;
(2)如图②,过点P作直线BC的垂线,垂足为E,当点P,Q分别在射线BA和AC的延长线上任意地移动过程中,线段BE,DE,CD中是否存在长度保持不变的线段?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠ABC>∠ADC,且∠BAD 的平分线 AE 与∠BCD 的平分线 CE 交于点 E,则∠AEC与∠ADC、∠ABC 之间存在的等量关系是( )

A. ∠AEC=∠ABC﹣2∠ADC B. ∠AEC=

C. ∠AEC=
 ∠ABC﹣∠ADC D. ∠AEC=
∠ABC﹣∠ADC D. ∠AEC= 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,BD、BE分别是高和角平分线,点F在CA的延长线上,FH⊥BE,交BD于点G,交BC于点H;下列结论:①∠DBE=∠F;②2∠BEF=∠BAF+∠C;③∠F=∠BAC-∠C;④∠BGH=∠ABE+∠C,其中正确的结论有___________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.
B.
C.
D.
相关试题

