【题目】已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的左边),与
的左边),与![]() 轴交于点
轴交于点![]() ,顶点为
,顶点为![]() .
.
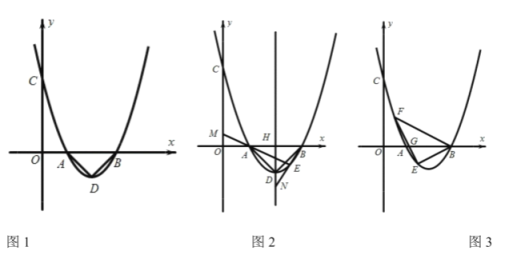
(1)如图1,请求出![]() 三点的坐标;
三点的坐标;
(2)点![]() 为
为![]() 轴下方抛物线
轴下方抛物线![]() 上一动点.
上一动点.
①如图2,若![]() 时,抛物线的对称轴
时,抛物线的对称轴![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交
交![]() 轴于点
轴于点![]() ,直线
,直线![]() 交对称轴
交对称轴![]() 于点
于点![]() ,求
,求![]() 的值;
的值;
②如图3,若![]() 时,点
时,点![]() 在
在![]() 轴上方的抛物线上运动,连接
轴上方的抛物线上运动,连接![]() 交
交![]() 轴于点
轴于点![]() ,且满足
,且满足![]() 当线段
当线段![]() 运动时,
运动时,![]() 的度数大小发生变化吗?若不变,请求出
的度数大小发生变化吗?若不变,请求出![]() 的值若变化,请说明理由.
的值若变化,请说明理由.
参考答案:
【答案】(1)![]() ;(2)①2; ②
;(2)①2; ②![]() =4,理由见解析
=4,理由见解析
【解析】
(1)令y=0,代入函数解析式,令x=0,代入函数解析式,即可求解;
(2)①过点![]() 作
作![]() 轴于点
轴于点![]() ,设点
,设点![]() ,由
,由![]() ,
,![]() ,得
,得![]() ,从而得
,从而得![]() ,进而即可得到结论;②设点
,进而即可得到结论;②设点![]() ,由题意得:
,由题意得:![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,作
,作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,由
,由![]() ,得
,得![]() ,从而得
,从而得![]() ,结合正切三角函数的定义,即可得到结论.
,结合正切三角函数的定义,即可得到结论.
(1)令y=0代入![]() ,得
,得![]() ,
,
解得:![]() ,
,
令x=0代入![]() ,得:y=3k,
,得:y=3k,
∴![]() ;
;
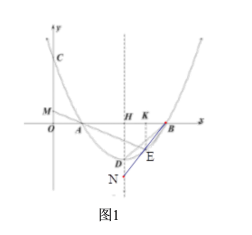
(2)①过点![]() 作
作![]() 轴于点
轴于点![]() ,如图1,则
,如图1,则![]() ,
,![]() ,
,
∵当![]() 时,
时,![]() ,对称轴为:直线x=2,
,对称轴为:直线x=2,
∴设点![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() ,
,
![]() ;
;
②不会变化,理由如下:
∵当![]() 时,
时,![]() ,
,
∴设点![]() ,
,
∵当![]() 时,不能满足
时,不能满足![]() ,
,
![]() ,
,
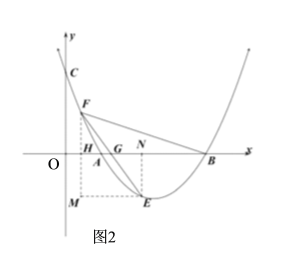
如图2,过点![]() 作
作![]() 轴于点
轴于点![]() ,作
,作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
∵![]() ,∠FHB=∠ENB=90°,
,∠FHB=∠ENB=90°,
![]() ,
,
![]() ,
,
![]() ,
,
∵EM∥x轴,
∴∠FGO=∠FEM,
![]()
∴点![]() 和点
和点![]() 在抛物线上运动时,
在抛物线上运动时,![]() 的值不会变化.
的值不会变化.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1)所示,一架长
 米的梯子
米的梯子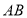 斜靠在与地面
斜靠在与地面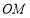 垂直的墙壁
垂直的墙壁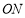 上,梯子与地面所成的角
上,梯子与地面所成的角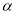 为
为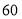 度.
度.(1)求图(1)中的
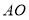 与
与 的长度;
的长度;(2)若梯子顶端
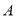 沿
沿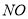 下滑,同时底端
下滑,同时底端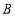 沿
沿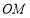 向右滑行.
向右滑行.①如图(2)所示,设
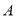 点下滑到
点下滑到 点,
点,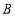 点向右滑行到
点向右滑行到 点,并且
点,并且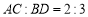 ,请计算
,请计算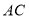 的长度;
的长度;②如图(3)所示,当
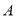 点下滑到
点下滑到 ,
,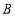 点向右滑行到
点向右滑行到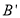 点时,梯子
点时,梯子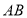 的中点
的中点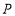 也随之运动到
也随之运动到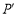 点,若
点,若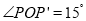 ,试求
,试求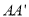 的长度.
的长度.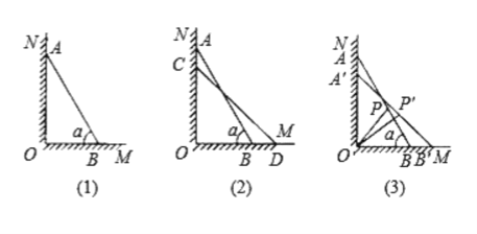
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以
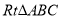 的直角边
的直角边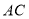 为直径作
为直径作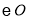 交斜边
交斜边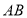 于点
于点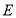 ,连接
,连接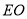 并延长交
并延长交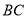 的延长线于点
的延长线于点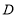 ,作
,作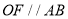 交
交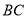 于点
于点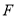 ,连接
,连接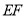 .
.(1)求证:
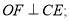
(2)求证:
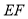 是
是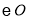 的切线;
的切线;(3)若
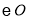 的半径为
的半径为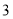 ,
,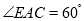 ,求
,求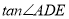 的值.
的值.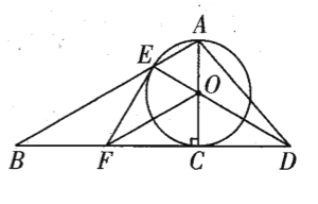
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,给出如下定义:已知两个函数,如果对于任意的自变量
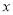 ,这两个函数对应的函数值记为
,这两个函数对应的函数值记为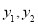 , 恒有点
, 恒有点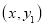 和点
和点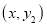 关于点
关于点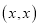 成中心对称(此三个点可以重合),由于对称中心
成中心对称(此三个点可以重合),由于对称中心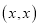 都在直线
都在直线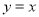 上,所以称这两个函数为关于直线
上,所以称这两个函数为关于直线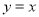 的“相依函数”。例如:
的“相依函数”。例如: 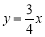 和
和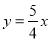 为关于直线
为关于直线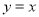 的 “相依函数”.
的 “相依函数”.(1)已知点
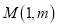 是直线
是直线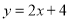 上一点,请求出点
上一点,请求出点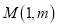 关于点
关于点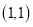 成中心对称的点
成中心对称的点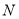 的坐标:
的坐标:(2)若直线
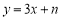 和它关于直线
和它关于直线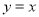 的“相依函数”的图象与
的“相依函数”的图象与 轴围成的三角形的面积为
轴围成的三角形的面积为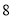 ,求
,求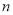 的值;
的值;(3)若二次函数
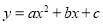 和
和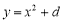 为关于直线
为关于直线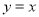 的“相依函数”.
的“相依函数”.①请求出
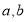 的值;
的值;②已知点
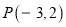 、点
、点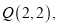 连接
连接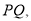 直接写出
直接写出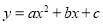 和
和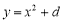 两条抛物线与线段
两条抛物线与线段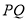 有目只有两个交占时对应的
有目只有两个交占时对应的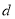 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示.则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点
 ,
,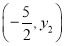 ,
,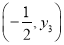 是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )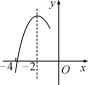
A.4B.3C.2D.1
-
科目: 来源: 题型:
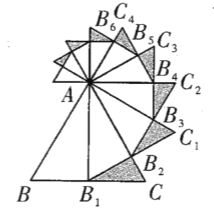
查看答案和解析>>【题目】如图,已知等边
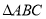 的边长是
的边长是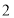 ,以
,以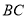 边上的高
边上的高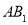 ,为边作等边三角形,得到第一个等边
,为边作等边三角形,得到第一个等边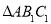 ;再以等边
;再以等边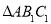 的
的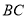 边上的高
边上的高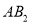 ,为边作等边三角形,得到第二个等边
,为边作等边三角形,得到第二个等边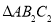 ,再以等边
,再以等边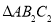 的
的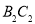 边上的高
边上的高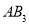 为边作等边三角形,得到第三个等边
为边作等边三角形,得到第三个等边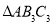 : ....记
: ....记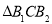 的面积为
的面积为 的面积为
的面积为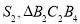 的面积为
的面积为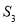 ,如此下去,则
,如此下去,则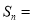 ___________
___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车,进行了一项油耗抽样实验:即在同一条件下,被抽样的该型号汽车,在油耗
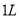 的情况下,所行驶的路程(单位:
的情况下,所行驶的路程(单位: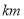 )进行统计分析,结果如图所示:
)进行统计分析,结果如图所示: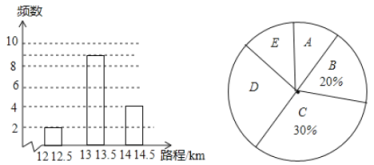
(注:记
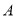 为
为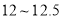 ,
, 为
为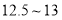 ,
,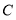 为
为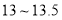 ,
,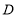 为
为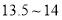 ,
,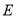 为
为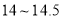 )
)请依据统计结果回答以下问题:
(1)试求进行该试验的车辆数;
(2)请补全频数分布直方图;
相关试题

