【题目】随着社会的发展,私家车变得越来越普及,使用节能低油耗汽车,对环保有着非常积极的意义,某市有关部门对本市的某一型号的若干辆汽车,进行了一项油耗抽样实验:即在同一条件下,被抽样的该型号汽车,在油耗![]() 的情况下,所行驶的路程(单位:
的情况下,所行驶的路程(单位:![]() )进行统计分析,结果如图所示:
)进行统计分析,结果如图所示:
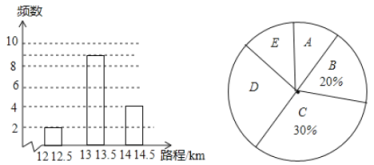
(注:记![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() ,
,![]() 为
为![]() )
)
请依据统计结果回答以下问题:
(1)试求进行该试验的车辆数;
(2)请补全频数分布直方图;
参考答案:
【答案】(1)30辆;(2)补图见解析
【解析】
(1)根据![]() 所占的百分比以及频数,即可得到进行该试验的车辆数;
所占的百分比以及频数,即可得到进行该试验的车辆数;
(2)根据![]() 的百分比,计算得到
的百分比,计算得到![]() 的频数,进而得到
的频数,进而得到![]() 的频数,据此补全频数分布直方图;
的频数,据此补全频数分布直方图;
(1)进行该实验的车辆数为:9÷30%=30(辆);
(2)B:20%×30=6(辆)D:30-2-6-9-4=9(辆)补全频数分布直方图如下:
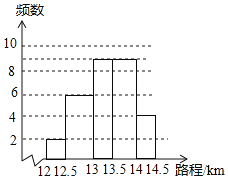
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
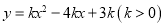 与
与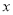 轴交于
轴交于 两点(点
两点(点 在点
在点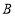 的左边),与
的左边),与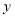 轴交于点
轴交于点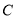 ,顶点为
,顶点为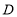 .
.(1)如图1,请求出
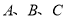 三点的坐标;
三点的坐标;(2)点
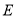 为
为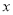 轴下方抛物线
轴下方抛物线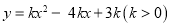 上一动点.
上一动点.①如图2,若
 时,抛物线的对称轴
时,抛物线的对称轴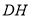 交
交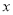 轴于点
轴于点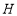 ,直线
,直线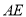 交
交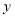 轴于点
轴于点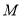 ,直线
,直线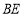 交对称轴
交对称轴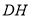 于点
于点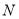 ,求
,求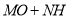 的值;
的值;②如图3,若
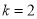 时,点
时,点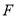 在
在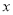 轴上方的抛物线上运动,连接
轴上方的抛物线上运动,连接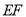 交
交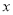 轴于点
轴于点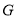 ,且满足
,且满足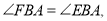 当线段
当线段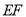 运动时,
运动时,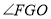 的度数大小发生变化吗?若不变,请求出
的度数大小发生变化吗?若不变,请求出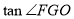 的值若变化,请说明理由.
的值若变化,请说明理由.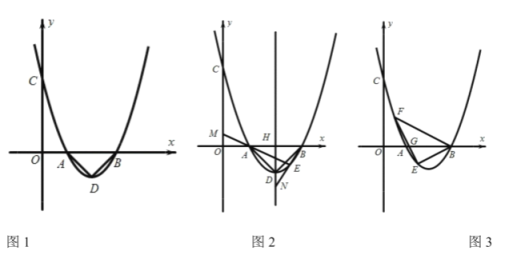
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示.则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点
 ,
,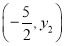 ,
,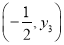 是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )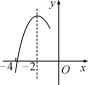
A.4B.3C.2D.1
-
科目: 来源: 题型:
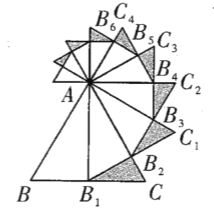
查看答案和解析>>【题目】如图,已知等边
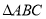 的边长是
的边长是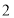 ,以
,以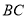 边上的高
边上的高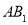 ,为边作等边三角形,得到第一个等边
,为边作等边三角形,得到第一个等边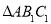 ;再以等边
;再以等边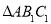 的
的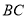 边上的高
边上的高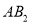 ,为边作等边三角形,得到第二个等边
,为边作等边三角形,得到第二个等边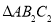 ,再以等边
,再以等边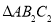 的
的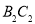 边上的高
边上的高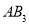 为边作等边三角形,得到第三个等边
为边作等边三角形,得到第三个等边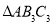 : ....记
: ....记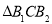 的面积为
的面积为 的面积为
的面积为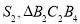 的面积为
的面积为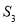 ,如此下去,则
,如此下去,则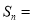 ___________
___________
-
科目: 来源: 题型:
查看答案和解析>>【题目】京杭大运河是世界文化遗产.综合实践活动小组为了测出某段运河的河宽(岸沿是平行的),如图,在岸边分别选定了点A、B和点C、D,先用卷尺量得AB=160m,CD=40m,再用测角仪测得∠CAB=30°,∠DBA=60°,求该段运河的河宽(即CH的长).
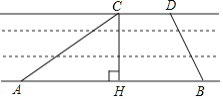
-
科目: 来源: 题型:
查看答案和解析>>【题目】为满足市场需求,某超市在五月初五“端午节”来临前夕,购进一种品牌粽子,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,每盒售价每提高1元,每天要少卖出20盒.
(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;
(2)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?
(3)为稳定物价,有关管理部门限定:这种粽子的每盒售价不得高于58元.如果超市想要每天获得不低于6000元的利润,那么超市每天至少销售粽子多少盒?
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名数学著作《周髀算经》中,为了方便,在本题中,我们把三边的比为3:4:5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15或3
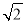 ,4
,4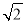 ,5
,5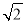 的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
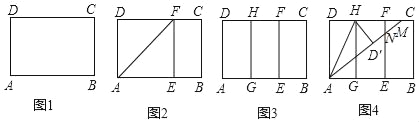
的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.实践操作 如图1,在矩形纸片ABCD中,AD=8cm,AB=12cm.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.
问题解决
(1)请在图2中证明四边形AEFD是正方形.
(2)请在图4中判断NF与ND′的数量关系,并加以证明;
(3)请在图4中证明△AEN(3,4,5)型三角形;
探索发现
(4)在不添加字母的情况下,图4中还有哪些三角形是(3,4,5)型三角形?请找出并直接写出它们的名称.
相关试题

