【题目】如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,
(1)请在图中标出△ABC的外接圆的圆心P的位置,并填写: 圆心P的坐标:P( , )
(2)将△ABC绕点A逆时针旋转90°得到△ADE,画出图形,并求△ABC扫过的图形的面积.
参考答案:
【答案】
(1)5,3
(2)解:根据图中信息由勾股定理可得: ![]() ,∴△ABC在旋转过程中扫过的面积为:S扇形ACE+S△ABC=
,∴△ABC在旋转过程中扫过的面积为:S扇形ACE+S△ABC= ![]() .
.

【解析】(1)三角形外接圆的圆心是三边垂直平分线的交点,因此作出边AB、BC的垂直平分线的交点,即可求出点P的坐标。
(2)根据旋转的性质,注意旋转的方向和旋转的角度画出旋转后的图形;观察图形可知,△ABC扫过的图形的面积=S扇形ACE+S△ABC,根据勾股定理求出AC的长后,即可算出结果。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2,以及对三角形的外接圆与外心的理解,了解过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心.
-
科目: 来源: 题型:
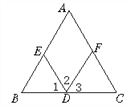
查看答案和解析>>【题目】如图,(1)∵∠A=_____(已知),
∴AC∥ED( )
(2)∵∠2=_____(已知),
∴AC∥ED( )
(3)∵∠A+_____=180°(已知),
∴AB∥FD( )
(4)∵AB∥_____(已知),
∴∠2+∠AED=180°( )
(5)∵AC∥_____(已知),
∴∠C=∠1( )
-
科目: 来源: 题型:
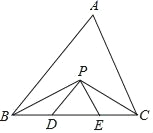
查看答案和解析>>【题目】如图,在△ABC中,BC=8cm,∠BPC=118°,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是_____cm,∠DPE=_____°.
-
科目: 来源: 题型:
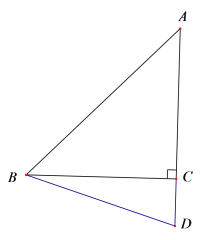
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠ACB=90°,D为AC延长线上一点,连接BD,在BC边上取一点E,使得CD=CE,连接AE并延长交BD于点F.
(1)依题意补全图形;
(2)求证:AF⊥BD;
(3)连接CF,点C 关于BD的对称点是Q,连接FQ,用等式表示线段CF,CQ之间的数量关系,并加以证明.
-
科目: 来源: 题型:
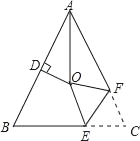
查看答案和解析>>【题目】如图,△ABC中,AB=AC,∠BAC=56°,∠BAC的平分线与AB的垂直平分线交于点O,将∠C沿EF(E在BC上,F在AC上)折叠,点C与点O恰好重合,则∠OEC为_____度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】交警通常根据刹车后轮滑行的距离来测算车辆行驶的速度,所用的经验公式是u=16
 .其中u表示车速(单位:km/h),d表示刹车距离(单位:m),f表示摩擦系数.在一次交通事故中,测得d=20m,f=1.44,而发生交通事故的路段限速为80km/h,肇事汽车是否违规超速行驶?说明理由.(参考数据:
.其中u表示车速(单位:km/h),d表示刹车距离(单位:m),f表示摩擦系数.在一次交通事故中,测得d=20m,f=1.44,而发生交通事故的路段限速为80km/h,肇事汽车是否违规超速行驶?说明理由.(参考数据: ≈1.4,
≈1.4, ≈2.2)
≈2.2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB、CD相交于O点,OM⊥AB;
(1)若∠1=∠2,求∠NOD;
(2)若∠1=
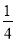 ∠BOC,求∠AOC与∠MOD.
∠BOC,求∠AOC与∠MOD.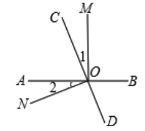
相关试题

