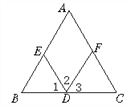
【题目】如图,(1)∵∠A=_____(已知),
∴AC∥ED( )
(2)∵∠2=_____(已知),
∴AC∥ED( )
(3)∵∠A+_____=180°(已知),
∴AB∥FD( )
(4)∵AB∥_____(已知),
∴∠2+∠AED=180°( )
(5)∵AC∥_____(已知),
∴∠C=∠1( )
参考答案:
【答案】(1)∠BED ; 同位角相等,两直线平行;(2)∠DFC ;内错角相等,两直线平行;(3)∠AFD;同旁内角互补,两直线平行;(4)DF;两直线平行,同旁内角互补;(5)ED;两直线平行,同位角相等;
【解析】
(1)∠BED ,同位角相等,两直线平行.
(2)∠DFC ,内错角相等,两直线平行.
(3)∠AFD ,同旁内角互补,两直线平行.
(4)DF ,两直线平行,同旁内角互补.
(5)ED ,两直线平行,同位角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B、C、D均在已知圆上,AD∥BC, AC平分∠BCD, 请找出图中与弦AD相等的线段,并加以证明

-
科目: 来源: 题型:
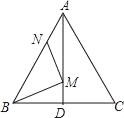
查看答案和解析>>【题目】如图,在等边△ABC中,AB=6,N为AB上一点,且AN=2,∠BAC的平分线交BC于点D,M是AD上的动点,连结BM,MN,则BM+MN的最小值是( )
A. 8 B. 10 C.
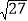 D. 2
D. 2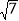
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC, D为直线BC上一动点(不与B,C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)当D在线段BC上时,求证:△BAD ≌△CAE;
(2)当点D运动到何处时,AC⊥DE,并说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,直接写出∠ADB的度数.


-
科目: 来源: 题型:
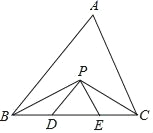
查看答案和解析>>【题目】如图,在△ABC中,BC=8cm,∠BPC=118°,BP、CP分别是∠ABC和∠ACB的平分线,且PD∥AB,PE∥AC,则△PDE的周长是_____cm,∠DPE=_____°.
-
科目: 来源: 题型:
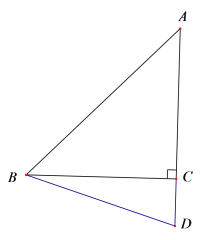
查看答案和解析>>【题目】如图,△ABC中,AC=BC,∠ACB=90°,D为AC延长线上一点,连接BD,在BC边上取一点E,使得CD=CE,连接AE并延长交BD于点F.
(1)依题意补全图形;
(2)求证:AF⊥BD;
(3)连接CF,点C 关于BD的对称点是Q,连接FQ,用等式表示线段CF,CQ之间的数量关系,并加以证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在10×10的正方形网格中(每个小正方形的边长都为1个单位),△ABC的三个顶点都在格点上.建立如图所示的直角坐标系,

(1)请在图中标出△ABC的外接圆的圆心P的位置,并填写: 圆心P的坐标:P( , )
(2)将△ABC绕点A逆时针旋转90°得到△ADE,画出图形,并求△ABC扫过的图形的面积.
相关试题

