【题目】如图,在ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE=![]() ∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是_____.
∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是_____.

参考答案:
【答案】①②③
【解析】
根据平行四边形的性质可得![]() ,再证明
,再证明![]() 是等腰三角形,根据等腰三角形的性质可得
是等腰三角形,根据等腰三角形的性质可得![]() ,进而得到
,进而得到![]() ;首先证明
;首先证明![]() ,再根据三角形中位线的性质可得
,再根据三角形中位线的性质可得![]() ,进而得到
,进而得到![]() ;证明
;证明![]() ,根据平行线的性质可得
,根据平行线的性质可得![]() ,再根据等边对等角可得
,再根据等边对等角可得![]() ,进而得到
,进而得到![]() .
.
①∵四边形ABCD是平行四边形,
∴![]()
∴![]()
∵![]() ,
,
∴![]()
∴![]()
∵E是CO中点![]()
∴![]()
∴![]()
故①正确;
②∵![]()
∴![]() 是等腰三角形,
是等腰三角形,
∵E是CO中点,
∴![]() ,
,
∴![]() ,
,
∵G为AB中点,
∴![]() ,
,
∵四边形ABCD是平行四边形,
∴AB=CD,
∵E、F分别OC、OD是的中点,
∴![]() ,
,
∴![]() ,
,
故②正确;
③∵E、F分别OC、OD是的中点,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
![]() ∠EFG=∠AGF,
∠EFG=∠AGF,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴GF平分![]() ,
,
故③正确;
④在![]() 中
中
∵G为AB的中点,
而BE与AE不一定相等,
∴EG与AB不一定垂直,
∵![]()
∴EF与GE不一定垂直,
故④错误;
综上:①②③正确,
故答案是:①②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=

 ,求⊙O半径的长.
,求⊙O半径的长.
-
科目: 来源: 题型:
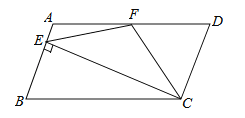
查看答案和解析>>【题目】如图,在□ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上(E不与A、B重合),连接EF、CF,则下列结论中一定成立的是 ( )
①∠DCF=
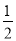 ∠BCD;②EF=CF;③
∠BCD;②EF=CF;③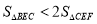 ;④∠DFE=4∠AEF.
;④∠DFE=4∠AEF.A. ①②③④ B. ①②③ C. ①② D. ①②④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合。将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.

(1)求证:△BPE∽△CEQ;
(2)求证:DP平分∠BPQ;
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个袋中均有三张除所标数值外完全相同的卡片,甲袋中的三张卡片上所标的数值分别为﹣7,﹣1,3,乙袋中的三张卡片上所标的数值分别为﹣2,1,6.先从甲袋中随机取出一张卡片,用x表示取出的卡片上标的数值,再从乙袋中随机取出一张卡片,用y表示取出的卡片上标的数值,把x、y分别作为点A的横坐标、纵坐标.
(1)用适当的方法写出点A(x,y)的所有情况;
(2)求点A落在第二象限的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部写出来,
的小数部分我们不可能全部写出来, ,于是可用
,于是可用 来表示
来表示 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:(1)
 的整数部分是________,小数部分是________.
的整数部分是________,小数部分是________.(2)如果
 的小数部分为
的小数部分为 ,
, 的整数部分为
的整数部分为 ,求
,求 的值.
的值.(3)已知:
 ,其中
,其中 是整数,且
是整数,且 ,求
,求 的相反数.
的相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,E、F 是平行四边形 ABCD 的对角线 AC 上的两点,AE=CF.

求证:(1)EB DF ;
(2)EB∥DF .
相关试题

