搜索
【题目】已知，如图，E、F 是平行四边形 ABCD 的对角线 AC 上的两点，AE=CF．
求证：（1）EB DF ；
（2）EB∥DF ．
参考答案：
【答案】（1）见解析；（2）见解析
【解析】
（1）由AE=CF，得到AF=CE，由平行四边形的性质，得出AD=CB，∠DAF=∠BCE，从而根据SAS推出两三角形全等，即可得到答案；
（2）由（1）可得到∠DFA=∠BEC，所以得到DF∥EB．
解：（1）∵AE=CF，
∴AE+EF=CF+FE，即AF=CE．
又ABCD是平行四边形，
∴AD=CB，AD∥BC．
∴∠DAF=∠BCE．
在△ADF与△CBE中
，
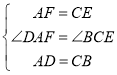∴△ADF≌△CBE（SAS）．
∴EB DF ；
（2）∵△ADF≌△CBE，
∴∠DFA=∠BEC．
∴DF∥EB．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在ABCD中，对角线AC、BD相交于点O，BD＝2AD，E、F、G分别是OC、OD、AB的中点，下列结论：①∠OBE＝
∠ADO；②EG＝EF；③GF平分∠AGE；④EF⊥GE，其中正确的是_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两个袋中均有三张除所标数值外完全相同的卡片，甲袋中的三张卡片上所标的数值分别为﹣7，﹣1，3，乙袋中的三张卡片上所标的数值分别为﹣2，1，6．先从甲袋中随机取出一张卡片，用x表示取出的卡片上标的数值，再从乙袋中随机取出一张卡片，用y表示取出的卡片上标的数值，把x、y分别作为点A的横坐标、纵坐标．
（1）用适当的方法写出点A（x，y）的所有情况；
（2）求点A落在第二象限的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】大家知道
是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部写出来，
，于是可用
来表示的小数部分.请解答下列问题：（1）
的整数部分是________，小数部分是________.（2）如果
的小数部分为
，
的整数部分为
，求
的值.（3）已知：
，其中
是整数，且
，求
的相反数. -
科目： 来源： 题型：
查看答案和解析>>【题目】某供暖部门为了解市民对2016年供暖情况的满意程度，对若干户市民进行了抽样调查（把市民对供暖情况的满意程度分为三个层次，A层次：满意；B层次：比较满意；C层次：不满意），将调查结果绘制成了如图所示的条形统计图和扇形统计图．
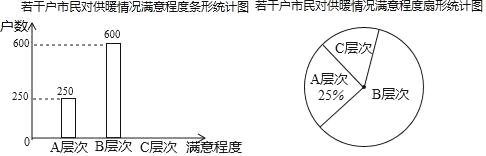
（1）请计算多少户市民参加了此次抽样调查，并补全条形统计图．
（2）根据抽样调查结果，请估计16000户市民中大约有多少户对2016年的供暖情况满意和比较满意．（包括A层次和B层次）
-
科目： 来源： 题型：
查看答案和解析>>【题目】一般地,二元一次方程的解可以转化为点的坐标,其中x的值对应为点的横坐标,y的值对应为点的纵坐标,如二元一次方程x2y=0的解
和
可以转化为点的坐标A(0,0)和B(2,1).以方程x2y=0的解为坐标的点的全体叫做方程x2y=0的图象。
(1)写出二元一次方程x2y=0的任意一组解___，并把它转化为点C的坐标___；
(2)在平面直角坐标系中，任何一个二元一次方程的图象都是一条直线，如方程x2y=0的图象是由该方程所有的解转化成的点组成，在图中描出点A. 点B和点C，观察它们是否在同一直线上；
(3)取满足二元一次方程x+y=3的两个解，并把它们转化成点的坐标，画出二元一次方程x+y=3的图象；
(4)根据图象,写出二元一次方程x2y=0的图象和二元一次方程x+y=3的图象的交点坐标___,由此可得二元一次方程组
的解是___. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知AM∥CN，点B为平面内一点，AB⊥BC于B.
(1)如图1，直接写出∠A和∠C之间的数量关系___；
(2)如图2，过点B作BD⊥AM于点D，求证：∠ABD=∠C；
(3)如图3,在(2)问的条件下,点E. F在DM上,连接BE、BF、CF,BF平分∠DBC,BE平分∠ABD,若∠FCB+∠NCF=180°，∠BFC=3∠DBE，求∠EBC的度数.
相关试题
