Question

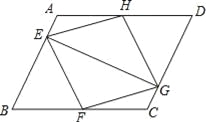
【题目】( 本小题满分10分)如图，已知：在平行四边形ABCD中，点E、F、G、H分别在边AB、BC、CD、DA上，AE=CG，AH=CF，且EG平分∠HEF．求证：

⑴△AEH≌△CGF；

⑵四边形EFGH是菱形．

Answer 1

【答案】（1）证明见试题解析；（2）证明见试题解析．

【解析】试题分析：(1)、由全等三角形的判定定理SAS证得结论；(2)、易证四边形EFGH是平行四边形，那么EF∥GH，那么∠HGE=∠FEG，而EG是角平分线，易得∠HEG=∠FEG，根据等量代换可得∠HEG=∠HGE，从而有HE=HG，易证四边形EFGH是菱形．

试题解析：（1）、如图，∵四边形ABCD是平行四边形， ∴∠A=∠C，

在△AEH与△CGF中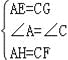，， ∴△AEH≌△CGF（SAS）；

(2)、∵四边形ABCD是平行四边形， ∴AB=CD，AD=BC，∠B=∠D． 又∵AE=CG，AH=CF，

∴BE=DG，BF=DH， 在△BEF与△DGH中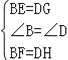，∴△BEF≌△DGH（SAS）， ∴EF=GH．

又由（1）知，△AEH≌△CGF， ∴EH=GF， ∴四边形EFGH是平行四边形， ∴HG∥EF，

∴∠HGE=∠FEG， ∵EG平分∠HEF， ∴∠HEG=∠FEG， ∴∠HEG=∠HGE， ∴HE=HG，∴四边形EFGH是菱形．