Question

【题目】如图，直线y=﹣x+3与x轴交于点C，与y轴交于点B，抛物线y=ax2+ x+c经过B、C两点，点E是直线BC上方抛物线上的一动点．

（1）求抛物线的解析式；
（2）过点E作y轴的平行线交直线BC于点M、交x轴于点F，当S△BEC= 时，请求出点E和点M的坐标；
（3）在（2）的条件下，当E点的横坐标为1时，在EM上是否存在点N，使得△CMN和△CBE相似？如果存在，请直接写出点N的坐标；如果不存在，请说明理由．

Answer 1

【答案】
（1）

解：∵直线y=﹣x+3与x轴交于点C，与y轴交于点B，

∴点B的坐标是（0，3），点C的坐标是（3，0），

∵y=ax2+ x+c经过B、C两点，

∴ ，解得： ，

∴y=﹣ x2+ x+3．

（2）

解：如图1，过点E作y轴的平行线EF交直线BC于点M，EF交x轴于点F，

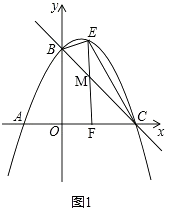
∵点E是直线BC上方抛物线上的一动点，

∴设点E的坐标是（x，﹣ x2+ x+3），

则点M的坐标是（x，﹣x+3），

∴EM=﹣ x2+ x+3﹣（﹣x+3）=﹣ x2+ x，

∴S△BEC=S△BEM+S△MEC= EMOC= ×（﹣ x2+ x）×3=﹣ x2+ x，

∴﹣ x2+ x= ，

解得，x1=1，x2=2，

即点E的坐标是（1，3）或（2，2），

此时对应的M的坐标是（1，2）或（2，1）．

（3）

解：存在．

∵B（0，3）、E（1，3），

∴BE=1，且BE∥OC，

由（1）知OB=OC=3，

∴∠BCO=∠CBE=∠CMN=45°，

∴CB=3 ，CM=2 ，

①当 = 时，△CMN∽△CBE，

即 = ，得MN= ，

∴FN= ，

∴N（1， ）；

②当 = 时，△CMN∽△EBC，

即 = ，得MN=12，

∴FN=﹣10，

N′（1，﹣10），

∴在EM上存在符合条件的点N，其坐标为（1， ）或（1，﹣10）．

【解析】（1）由直线y=﹣x+3求得点B、C坐标，代入抛物线解析式求得b、c即可得；（2）设E（x，﹣ x2+ x+3），则M（x，﹣x+3），可知EM=﹣ x2+ x，根据S△BEC=S△BEM+S△MEC= EMOC= 列出关于x的方程，解之可得答案；（3）由题意得出∠BCO=∠CBE=∠CMN=45°、BE=1、CB=3 、CM=2 ，根据 = 和 = 分别求出MN即可得．
【考点精析】本题主要考查了二次函数的性质的相关知识点，需要掌握增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大增大；对称轴右边，y随x增大而减小才能正确解答此题．