【题目】已知关于![]() 的一元二次方程x2-(k+2)x+k-1=0
的一元二次方程x2-(k+2)x+k-1=0
(1)若方程的一个根为 -1,求![]() 的值和方程的另一个根;
的值和方程的另一个根;
(2)求证:不论![]() 取何值,该方程都有两个不相等的实数根.
取何值,该方程都有两个不相等的实数根.
参考答案:
【答案】(1)k= -1,另一根为x=2;(2)见解析.
【解析】
(1)把x=-1代入方程可求得k的值,再解方程可求得另一根;
(2)由方程根的情况可得到关于m的不等式,可求得m的取值范围.
(1)把x=-1代入方程可得1+(k+2)+k-1=0,
解得k=-1,
当k=-1时,原方程为x2-x-2=0,
解得x1=-1,x2=4,
即k的值为-1,方程的另一根为4;
(2)∵a=1,b=-(k+2),c=k-1,
∴△=b2-4ac=[=-(k+2)]2-4×1×(k-1)=k2+8>0,
∴不论k为何值时,方程总有两个不相等的实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,OA1=1,将边长为1的正方形一边与x轴重合按图中规律摆放,其中每两个正方形的间距都是1,则点A2017的坐标为 .
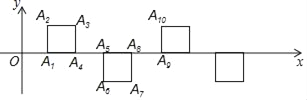
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频率分布表和频率直方图的一部分如下:
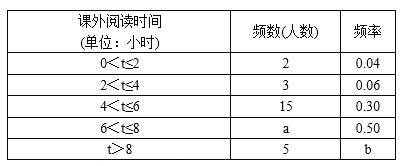
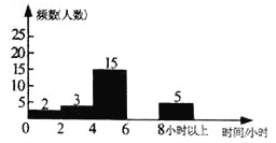
请根据图表信息回答下列问题:
(1)频数分布表中的a=____________,b=____________;
(2)将频数直方图补充完整;
(3)学校将每周课外阅读时间在6小时以上的学生评为“阅读之星”,请你估计该校2 000名学生中评为“阅读之星”的有多少人?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:

(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着济宁旅游业的快速发展,外来游客对住宿的需求明显增大,某宾馆拥有的床位数不断增加。
(1)该宾馆床位数从2016年底的200个增长到2018年底的242个,求该宾馆这两年(从2016年底到2018年底)拥有的床位数的年平均增长率。
(2)根据市场表现发现每床每日收费40元,242张床可全部租出,若每床每日收费提高10元,则租出床位减少20张。若想平均每天获利11100元,同时又减轻游客的经济负担,每张床位应定价多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,点C在AOB的一边OA上,过点C的直线DE//OB,CF平分ACD,CG CF于C .
(1)若O =40,求ECF的度数;
(2)求证:CG平分OCD;
(3)当O为多少度时,CD平分OCF,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式。求解二元一次方程组,把它转化为一元一次方程来解:求解一元二次方程,把它转化为两个一元一次方程来解。求解分式方程,把它转化为整式方程来解。各类方程的解法不尽相同,但是它们有一个共同的基本数学思想--转化,把未知转化为已知。
用“转化”的数学思想,我们还可以解一些新的方程。例如,一元三次方程
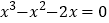 ,可以通过因式分解把它转化为
,可以通过因式分解把它转化为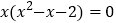 ,解方程
,解方程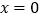 和
和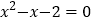 ,可得方程
,可得方程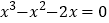 的解。
的解。(1)问题:方程
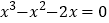 的解是
的解是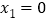 ,
,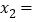 _____,
_____,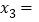 _____。
_____。(2)拓展:用“转化”思想求方程
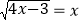 的解。
的解。(3)应用:如图,已知矩形草坪ABCD的长
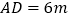 ,宽
,宽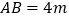 ,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C。求AP的长。
,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C。求AP的长。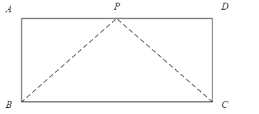
相关试题

