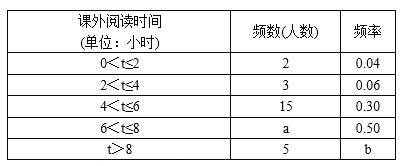
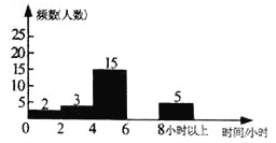
【题目】为了加强学生课外阅读,开阔视野,某校开展了“书香校园,从我做起”的主题活动,学校随机抽取了部分学生,对他们一周的课外阅读时间进行调查,绘制出频率分布表和频率直方图的一部分如下:
请根据图表信息回答下列问题:
(1)频数分布表中的a=____________,b=____________;
(2)将频数直方图补充完整;
(3)学校将每周课外阅读时间在6小时以上的学生评为“阅读之星”,请你估计该校2 000名学生中评为“阅读之星”的有多少人?
参考答案:
【答案】(1)a=25;b=0.1;(2)见解析;(3)1200.
【解析】
第一问:因为知道a所对应的的频率,所以先找总数,2对应的频率为0.04,就用2÷0.04=50,所以总数有50人,50×0.5=25,所以a=25,![]()
第二问:将6-8的25补上即可,答案见详解
第三问:因为6小时以上的频率为0.50+0.10=0.60,2000×0.60=1200人
解:(1) 频数分布表中的a=__25__________,b=____0.1________;
(2) 补充直方图:
(3) 0.50+0.10=0.60,2000×0.60=1200人
-
科目: 来源: 题型:
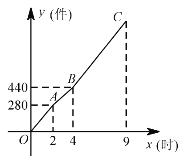
查看答案和解析>>【题目】某玩具厂加工了一批玩具“六一”捐赠给儿童福利院,甲、乙两车间同时开始加工这批玩具,加工一段时间后,甲车间的设备出现故障停产一段时间,乙车间继续加工,甲维修好设备后继续按照原来的工作效率加工,从工作开始到加工完这批玩具乙车间工作
 小时,甲、乙两车间加工玩具的总数量
小时,甲、乙两车间加工玩具的总数量 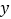 (件)与加工时间
(件)与加工时间  (时)之间的函数图象如图所示.
(时)之间的函数图象如图所示.(1)求乙车间每小时加工玩具的数量.
(2)求甲车间维修完设备后,
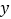 与
与  之间的函数关系式.
之间的函数关系式.(3)何时能加工一半?
-
科目: 来源: 题型:
查看答案和解析>>【题目】当
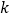 值相同时,我们把正比例函数
值相同时,我们把正比例函数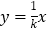 与反比例函数
与反比例函数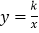 叫做“关联函数”,可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以
叫做“关联函数”,可以通过图象研究“关联函数”的性质.小明根据学习函数的经验,先以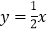 与
与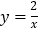 为例对“关联函数”进行了探究.下面是小明的探究过程,请你将它补充完整.
为例对“关联函数”进行了探究.下面是小明的探究过程,请你将它补充完整.(1)如图,在同一坐标系中画出这两个函数的图象.设这两个函数图象的交点分别为
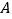 ,
,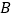 ,则点
,则点 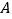 的坐标为
的坐标为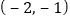 ,点
,点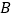 的坐标为_______;
的坐标为_______;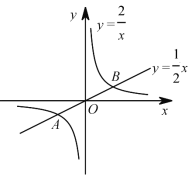
(2)点
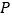 是函数
是函数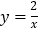 在第一象限内的图象上一个动点(点
在第一象限内的图象上一个动点(点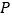 不与点
不与点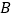 重合),设点
重合),设点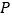 的坐标为
的坐标为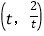 ,其中
,其中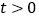 且
且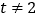 .
.①结论
 :作直线
:作直线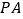 ,
,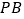 分别与
分别与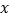 轴交于点
轴交于点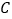 ,
,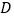 ,则在点
,则在点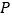 运动的过程中,总有
运动的过程中,总有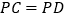 .
.证明:设直线
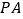 的解析式为
的解析式为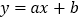 ,将点
,将点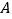 和点
和点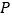 的坐标代入,得
的坐标代入,得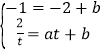
解得
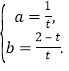 则直线
则直线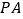 的解析式为
的解析式为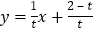 .
.令
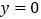 ,可得
,可得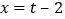 ,则点
,则点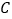 的坐标为
的坐标为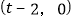 .
.同理可求,直线
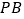 的解析式为
的解析式为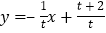 ,点
,点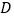 的坐标为________.
的坐标为________.请你继续完成证明
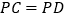 的后续过程:
的后续过程:②结论
 :设
:设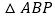 的面积为
的面积为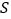 ,则
,则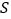 是
是 的函数.请你直接写出
的函数.请你直接写出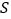 与
与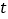 的函数表达式.
的函数表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系中,OA1=1,将边长为1的正方形一边与x轴重合按图中规律摆放,其中每两个正方形的间距都是1,则点A2017的坐标为 .
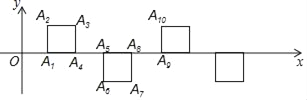
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三角形DEF是三角形ABC经过某种变换得到的图形,点A与点D,点B与点E,点C与点F分别是对应点,观察点与点的坐标之间的关系,解答下列问题:

(1)分别写出点A与点D,点B与点E,点C与点F的坐标,并说说对应点的坐标有哪些特征;
(2)若点P(a+3,4-b)与点Q(2a,2b-3)也是通过上述变换得到的对应点,求a,b的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于
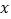 的一元二次方程x2-(k+2)x+k-1=0
的一元二次方程x2-(k+2)x+k-1=0(1)若方程的一个根为 -1,求
 的值和方程的另一个根;
的值和方程的另一个根;(2)求证:不论
 取何值,该方程都有两个不相等的实数根.
取何值,该方程都有两个不相等的实数根. -
科目: 来源: 题型:
查看答案和解析>>【题目】随着济宁旅游业的快速发展,外来游客对住宿的需求明显增大,某宾馆拥有的床位数不断增加。
(1)该宾馆床位数从2016年底的200个增长到2018年底的242个,求该宾馆这两年(从2016年底到2018年底)拥有的床位数的年平均增长率。
(2)根据市场表现发现每床每日收费40元,242张床可全部租出,若每床每日收费提高10元,则租出床位减少20张。若想平均每天获利11100元,同时又减轻游客的经济负担,每张床位应定价多少元?
相关试题

